5. 数据安全:防御¶
本章节介绍针对数据投毒、隐私攻击、数据窃取和篡改与伪造的防御方法。防御比攻击更有挑战性,防御者不但需要抵御目前已知的所有攻击,还要能抵御适应性攻击和未来不可知的攻击。由于攻击类型的多样性、不同攻击间的巨大差异性、攻击的快速迭代性等因素,数据安全方面的防御工作目前还停留在定点防御的阶段,主要针对某种已知攻击设计防御方法,在防得住一种(或一类)攻击的基础上力争兼顾其他攻击类型。下面讲围绕几种数据攻击介绍对应的防御方法。
5.1. 鲁棒训练¶
“数据有问题,算法来补救”。应对数据投毒最直接的一种防御方法就是鲁棒训练,即提高训练算法的鲁棒性,使其能够在训练过程中检测并抛弃毒化样本,从而避免模型被攻击。可惜的是此方面的研究工作并不是很多。我们在很多时候并不知道数据是否被投毒,也无法估计被投毒的比例有多大、样本有哪些,所以也就很难设计高效的鲁棒训练方法。但随着大规模预训练的流行,此类的鲁棒训练算法将会变的格外重要。
Shen等人 (Shen and Sanghavi, 2019) 系统的研究了三种问题数据,包括分类任务中的噪声标签(标签存在错误)、对抗生成任务中的污染数据(一个数据集里出现了别的数据集的样本)和分类任务中的后门投毒样本。研究者通过实验发现“好”的数据往往学的更快,即训练损失下降更快,并基于此提出一种基于修剪损失( trimmed loss)的鲁棒训练方法,让模型只在好的样本上进行学习。基于修剪损失的模型训练所对应的优化问题如下:
其中,\(\mathfrak{B}\)表示模型的紧致参数空间(compact parameter space),比原参数空间要小,\(S\)是内层最小化问题寻找到的样本子集,实际上就是训练损失很小的\(\lfloor\alpha n\rfloor\)个样本,\(\alpha\)是比例,\(n\)是原训练集样本数量。可以看出这是一个min-min双层优化问题,内部最小化问题寻找一部分损失最小的样本子集,然后在这个样本子集上训练得到干净的模型。此方法在三个问题数据场景下都取得了不错的效果,其中包括基于简单后门攻击BadNets (Chan et al., 2022) 的数据投毒。
此外,由于投毒样本往往只占训练数据很小的一部分,那么这些样本就可以通过数据划分(partition)隔离出来。将训练数据集划分成一定数量的子集,通过恰当的设置子集的大小可以让划分得到的子集大部分都是干净子集(即不包括任何投毒样本)。我们在干净子集上训练得到的模型都是干净(子)模型,基于这些模型我们就可以以投票的方式得到干净无毒的预测结果。
基于上述思想,Levine等人 (Levine and Feizi, 2021) 提出可以理论证明的投毒防御方法:深度划分聚合(deep partition aggregation,DPA)。具体的,令\(\mathcal{S}_L:=\{( x,c)| x \in \mathcal{S},c\in \mathbb{N} \}\)为有类标的样本集,\(\mathcal{S}\)为无类标的样本空间。一个供模型训练的训练集可表示为:\(\mathcal{T}\in \mathcal{P}(\mathcal{S}_L)\),其中\(\mathcal{P}(\mathcal{S}_L)\)是集合\(\mathcal{S}_L\)的幂集。对于\(t\in \mathcal{S}_L\),令\(sample( t)\in \mathcal{S}_L\)为数据样本,\(label(t)\in \mathbb{N}\)为标签。一个分类模型被定义为由有标签的训练集和无(待定)标签的数据集共同确定的函数:\(f:\mathcal{P}(\mathcal{S}_L) \times \mathcal{S}\to \mathbb{N}\)。令\(f(\cdot)\)表示(不鲁棒的)基分类模型,\(g(\cdot)\)表示鲁棒的分类模型。 DPA算法需要一个哈希函数\(h:\mathcal{S}_L\to \mathbb{N}\)和超参数\(k\in \mathbb{N}\)表示用于集成的基本分类器个数。在训练阶段,DPA首先用哈希函数将训练集\(\mathcal{T}\)划分为\(k\)个子集,分别为\(P_1,\ldots,P_k\in \mathcal{T}\):
在选择哈希函数\(h(\cdot)\)时,最好可以使各子集的大小一致。对于图像数据,\(h( t)\)为图像\(t\)的像素值之和。基于子集划分,我们可以在每个子集训练一个基分类器,定义如下:
在推理阶段,我们可以每个基分类器进行预测,并统计有多少个基分类器将输入样本分类为\(c\):
最终,DPA选择大部分基分类器都同意的类别作为其鲁棒预测类别:
Li等人 (Li et al., 2021) 对十种后门投毒攻击进行了研究,发现了跟之前的工作 (Shen and Sanghavi, 2019) 不太一样的结论:后门投毒样本往往被学习的更快而不是更慢。这主要是因为后门攻击需要在触发器样式和后门类别之间建立强关联,而这种强关联使得后门样本损失下降的更快。基于此观察,研究者提出训练阶段后门投毒防御方法“反后门学习”(anti-backdoor learning,ABL)。ABL方法将会在后门防御章节 9节 中进行详细的介绍,这里简单描述一下它的主要思想。ABL将模型训练分为两个阶段,在第一阶段通过局部梯度上升(local gradient ascent,LGA)技术检测和隔离投毒样本,在第二个阶段通过全局梯度上升(global gradient ascent,GGA)技术对隔离出来的投毒样本进行反学习。局部梯度上升通过约束训练样本的损失下限来阻止干净样本产生过低的训练损失,而后门样本由于其强关联性会突破这个限制,依然产生更低的损失。所以局部梯度上升相当于一个筛子,将后门样本过滤出来。第二阶段的全局梯度上升通过最大化模型在所检测投毒样本子集上的损失来“反学习”掉后门关联。这一步后门反学习是有必要的,因为当后门样本被检测出来的时候也就意味着模型已经学习了后门(因为否则就无法知道某个样本是否是后门样本)。
Yang等人 (Yang et al., 2022) 观察中毒样本发现,并不是所有中毒样本对攻击是有效的(即现有攻击往往投毒更多一些的样本来确保攻击成功)。基于此观察,研究者提出了有效毒药(effective poisons)的概念,来指代在删除其他的中毒样本的情况下也能让模型中毒的最小投毒样本子集。有趣的是,观察发现有效毒药并不是决策边界附近的中毒样本,也不是比同类样本具有更高损失的离群点。投毒攻击的主要策略是对原始样本添加扰动(噪声和图案都可以看做是一种扰动),使得中毒样本的梯度在模型训练过程中远离正确类别,靠近攻击目标类别。 虽然扰动的目的都是让原始梯度变为目标梯度,但是不同类型的有效毒药之间都有着不同的修改轨迹。同时,在训练过程中,随着有效毒药和目标类别之间梯度相似度的提高,有效毒药的梯度信息也会变的明显有别于干净样本。因此,在训练的早期,就可以在梯度空间中把有效毒药的梯度孤立出来,如借助k-medoids聚类算法进行孤立点的检测,成为防御投毒攻击的主要突破口。
在模型训练过程中使用数据增强也可以在一定程度上打破投毒样本与投毒目标之间的关联。例如,Borgnia等人 (Borgnia et al., 2021) 研究发现常用数据增强方法,如Mixup (Zhang et al., 2018) 、CutMix (DeVries and Taylor, 2017) 以及MaxUp (Gong et al., 2020) 等,不仅可以有效降低投毒和后门攻击的威胁,且会给模型带来更好的性能。这使得数据增强成为鲁棒训练的一个关键部分。大胆猜测,未来更高效的鲁棒训练算法将会以某种数据增强的方式出现。
5.2. 差分隐私¶
5.2.1. 差分隐私概念¶
差分隐私(differential privacy,DP)的概念是由Dwork等人 (Dwork, 2006) 在2006年提出的,其来源于密码学中的语义安全(semantic security),即明文完成加密后攻击者无法区分不同明文对应的密文。差分隐私在传统数据发布(data release)领域的隐私保护方面有着优异的表现,被广泛应用于各类相关的软件产品中,如苹果公司的iOS10系统在其输入法和搜索功能中使用差分隐私技术来收集用户键盘、Notes以及Spotlight的数据 (Novac et al., 2017) 。
差分隐私保护的主体并不是数据集整体的隐私,而是其中单个个体的隐私,因此,差分隐私要求数据集中单个个体对相关函数的输出影响都在一定的限度之内。差分隐私最早被用于数据查询业务,对此Dwork等人 (Dwork, 2006) 提出了相邻数据集(neighboring datasets)的概念,即只差一条记录的两个数据集称为相邻数据集,如有数据集A:{小明,小王,小赵},B:{小王,小赵}和C:{小李,小王,小赵},则A与B或A与C都称为相邻数据集。差分隐私有着非常严格的数学原理,相关概念定义如下。
定义 差分隐私:对于一个随机算法\(M\),\(P_m\)为算法\(M\)所有可能输出的集合,若算法\(M\)满足\(( \epsilon,\delta)-DP\),当且仅当相邻数据集\(D\),\(D'\)对\(M\)的所有可能输出子集\(S_m\in P_m\),满足不等式 (Dwork et al., 2006) :
上式中,\(\epsilon\)称为隐私预算(privacy budget),\(\epsilon\)越小则隐私预算越低,意味着差分隐私算法使得查询函数在一对相邻数据集上返回结果的概率分布越相似,故而隐私保护程度越高。\(\delta\)表示打破\(( \epsilon,\delta)-DP\)限制的可能性,当\(\delta=0\)时,可称为\(\epsilon-DP\),此时的隐私保护更加严格。
差分隐私有两条非常重要的合成性质,分别为顺序合成和平行合成 (McSherry, 2009) 。
性质 顺序合成:给定\(K\)个随机算法\(M_i(i=1,\ldots,K)\),分别满足\(\epsilon_i-DP\),如果将他们作用在同一个数据集上,则满足\(\sum_{i=1}^K \epsilon_i-DP\)。
性质 平行合成:将数据集\(D\)分割成\(K\)个不相交的子集\(\{D_1,D_2,\ldots,D_K\}\),在每个子集上分别作用满足\(\epsilon_i-DP\)的随机算法\(M_i\),则数据集\(D\)整体满足\((\max\{ \epsilon_1,\ldots, \epsilon_K\})-DP\)。
顺序合成表明,将多个算法组成的序列同时作用在一个数据集上,最终的隐私预算等于算法序列中单个算法隐私预算的总和。平行合成表明,当多个算法分别作用在一个数据集的不同子集上时,整体的隐私预算为所有算法隐私预算的最大值。
2010年,Kifer等人 (Kifer and Lin, 2010) 又为差分隐私提出了两条重要性质,分别为交换不变性和中凸性。
性质 交换不变性:给定任意算法\(M_1\)满足\(\epsilon-DP\)、数据集\(D\),对于任意算法\(M_2\)(\(M_2\)不一定满足差分隐私),则\(M_2(M_1(D))\)满足\(\epsilon-DP\)。
性质 中凸性:给定满足\(\epsilon-DP\)的随机算法\(M_1\)和\(M_2\),对于任意的概率\(P\in[0,1]\),用\(A_P\)表示一种选择机制,以\(P\)的概率选择算法\(M_1\),以\(1-P\)的概率选择算法\(M_2\),则\(A_P\)机制满足\(\epsilon-DP\)。
在了解完差分隐私的基本概念之后,我们要思考的问题是如何构建差分隐私模型。在查询任务中,差分隐私是通过给查询结果添加噪声来完成隐私保护的,添加的噪声越多对隐私信息的保护会更好,但同时也会使得查询结果的可用性降低。因此,噪声的添加量是一个非常重要的参数。函数敏感度则为噪声的添加量提供了依据,所以Dwork等人 (Dwork et al., 2006) 在其2006年的工作中提出使用全局敏感度来控制噪声添加量。
定义 全局敏感度(global sensitivity):给定查询函数\(f:D\to R\),其中\(D\)为数据集,\(R\)为查询结果。在任意一对相邻数据集\(D\),\(D'\)上,全局敏感度定义为:
其中,\(\|f(D)-f(D') \|_1\)表示\(f(D)\)与\(f(D')\)之间的曼哈顿距离。
然而,根据全局敏感度所添加的噪声量会对数据产生过度的保护,从而影响数据的可用性。对此,Nissim等人 (Nissim et al., 2007) 提出了局部感度的概念。
定义 局部敏感度(local sensitivity):给定查询函数\(f:D\to R\),\(D\)为数据集,\(R\)为查询结果。在任意一对相邻数据集\(D\),\(D'\)上,局部敏感度定义为:
比较公式 (5.2.2) 和 (5.2.3) 可以看出,局部敏感度只是针对一个特定数据集\(D\)而言的,而全局敏感度则涵盖任意数据集。
了解完噪声添加量的控制,添加何种噪声又成为我们不得不思考的问题。添加的噪声类型会对结果产生直接的影响。因此,接下来我们将介绍几种被广泛使用的噪声添加机制,分别为拉普拉斯机制 (Dwork, 2011) 、高斯机制 (Dwork et al., 2014) 和指数机制 (McSherry and Talwar, 2007) 。
(1)拉普拉斯机制:给定一个函数\(f:D\to R\),对其函数的输出加入符合特定拉普拉斯分布的噪声,则可使机制\(M\)满足\(\epsilon-DP\):
其中,\(Lap(\frac{S(f)}{ \epsilon})\)表示位置参数为0,尺度参数为\(\frac{S(f)}{ \epsilon}\)的拉普拉斯分布,\(S(f)\)为函数\(f\)的敏感度。
(2)高斯机制:对于函数\(f:D\to R\),若要使其满足\(( \epsilon,\delta)-DP\),则在函数输出值上加入符合相应分布的高斯噪声:
其中,\(\mathcal{N}(\delta^2)\)表示中心为0,方差为\(\delta^2\)的高斯分布,,\(S(f)\)为函数\(f\)的敏感度。高斯机制与拉普拉斯机制除了分布本身的不同,高斯机制满足的是\(( \epsilon,\delta)-DP\),相比拉普拉斯机制更宽松一些。
(3)指数机制:前两种机制通过直接在函数输出值上添加噪声来完成差分隐私,主要应对的是数值型函数。而指数机制应对的则是非数值函数,通过概率化输出值来完成差分隐私。例如对于一个查询函数\(f\),其输出值是一组离散数据\(\{R_1,R_2,\ldots,R_N\}\)中的元素,指数机制的思想是对于\(f\)的输出值,不是确定性的\(R_i\),而是以一定的概率返回结果。因此会涉及到计算概率值的打分函数\(q(D,R_i)\),\(D\)为数据集,\(q(D,R_i)\)为输出结果为\(R_i\)的分数,若要使机制\(M\)满足\(\epsilon-DP\),则有:
其中,\(S(q)\)为函数\(q\)的敏感度。对其归一化则可以得到输出值\(R_i\)的概率:
5.2.2. 差分隐私在深度学习中的应用¶
深度学习模型的过度参数化使其很容易发生过拟合,在无意中记忆大量训练数据的隐私信息,给成员推理、数据窃取等数据攻击留下了可乘之机,给模型在实际场景中的部署应用带来巨大的隐私泄露隐患。差分隐私作为一种具有严格数据证明的隐私保护方法,可有效保护深度学习模型的隐私泄露问题,本节根据差分隐私在深度学习模型上应用位置的不同,从输入层、隐藏层和输出层三个层面展开介绍一些经典的防御算法。
5.2.2.1. 输入空间:差分隐私预处理训练数据¶
差分隐私部署在输入层意味着在差分隐私机制下生成合成数据(synthesized data),并用合成数据替换原始数据用于模型训练。为了得到可用的合成数据,一个经典方法是借助生成模型:利用原始数据训练一个生成模型,负责生成与原始数据具有相同统计分布的合成数据。而差分隐私机制则通过在生成模型中添加噪声来完成,噪声的添加方法以及隐私预算计算方法距会计(moments accountant)将在隐藏层部分进行详细介绍。
Su等人 (Su et al., 2017) 利用k-means聚类算法先将原始数据分成\(K\)个类,然后分别在\(K\)个类上借助差分隐私机制训练\(K\)个生成模型,如变分自编码器(variational autoencoder,VAE),并将\(K\)个生成模型集成得到最终的生成模型。聚类的目的是将具有相同特征的数据集中在一起,有助于生成模型的训练。之后也有学者利用生成对抗网络(GAN)提出dp-GAN (Zhang et al., 2018) (框架如图 dp-GAN框架图 zhang2018differentially 所示)来生成数据。管理者基于收集到的数据利用差分隐私训练生成模型,最后利用生成模型的合成数据完成分析任务。其中,差分隐私只应用在GAN的判别器的训练过程中,差分隐私机制的实施借助于噪声添加和梯度裁剪两种方法(将在下面进行介绍)。
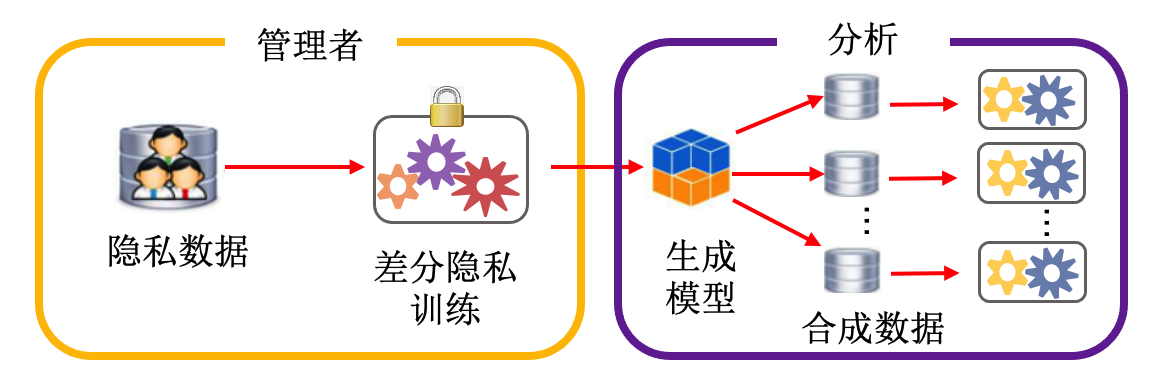
图5.2.1 dp-GAN框架图 (Zhang et al., 2018)¶
5.2.2.2. 隐藏空间:差分隐私平滑模型参数¶
深度学习模型的参数携带着训练数据的大量隐私信息,为了防止训练数据隐私信息的泄露,最直接的方法是平滑深度学习模型的参数。然而,模型参数对训练数据的依赖性很难厘清,因此对模型参数在差分隐私机制下添加严格的噪声,会降低模型的可用性。对此,Abadi等人 (Abadi et al., 2016) 提出了差分隐私随机梯度下降(differentially private SGD,DP-SGD)算法,将差分隐私嵌入到机器学习模型的训练过程去,通过对梯度信息的保护达到对最终模型的保护,其思路如算法 图5.2.2 所示。

图5.2.2 算法 Differentially Private SGD(DP-SGD) (Abadi et al., 2016)¶
DP-SGD算法以批量梯度下降为基础,通过计算一组数据的平均梯度得到真实梯度的无偏估计。为了区别于传统的批训练,DP-SGD提出了分组(lot)的概念,每个组含有\(L\)个数据样本,以概率\(L/n\)进行独立采样,但是组的大小大于批,一个分组可看作由多批样本组成,组是添加噪声的基本单位。算法 图5.2.2 的核心部分为梯度裁剪和噪声添加。除此之外,为保证算法总体满足\(( \epsilon,\delta)-DP\),Abadi等人提出了距会计(moments accountant,MA)算法。接下来将分别介绍这三个核心技术。
(1)梯度裁剪: 梯度裁剪经常被用来处理梯度消失或爆炸问题,但在DP-SGD算法中它的目的是限制单个样本对模型参数的影响,以确保严格的差分隐私。DP-SGD对每个样本梯度的\(L_2\)范数进行裁剪,设定阈值\(C\):当\(\|g\|_2<C\)时,原始梯度\(g\)被保留;当\(\|g\|_2>C\)时,将按一定比例缩小。
选取阈值\(C\)时需要权衡两个对立的影响。首先,裁剪会破坏梯度的无偏估计,如果裁剪阈值过小,则裁剪后的梯度会指向与真实梯度完全不同的方向。其次,后续噪声的添加过程也是依据\(C\)进行的,因此增加\(C\)会使得在梯度中添加过多的噪声,影响最终模型的可用性。因此,一个简单可行的方法是将其设定为未裁剪梯度范数的中值。
(2)噪声添加: DP-SGD利用高斯噪声机制完成\(( \epsilon,\delta)-DP\),噪声添加在一个分组的平均梯度之上:
其中,\(\mathcal{N}(0,\sigma^2C^2{I})\)表示均值为0,标准差为\(C \cdot \sigma\)的高斯分布,\({I}\)为与梯度维度相同的单位矩阵。对于高斯机制的差分隐私,若设定此处的\(\sigma\):
则可以让每一个分组都满足\(( \epsilon,\delta)-DP\)(Dwork et al., 2014) 。
(3)隐私损失计算: DP-SGD算法的关键是计算训练过程的隐私损失。有差分隐私的合成性质可知:只要能够得到训练过程中每一步的隐私损失,通过累加就可以得到总体隐私损失。深度学习模型在计算隐私损失时需要考虑多层的梯度以及所有与梯度相关联的隐私预算,因此是否可以有效准确的统计隐私成为决定差分隐私机制效果的关键。距会计(MA)是差分隐私机器学习领域最常用也是最优越的隐私损失计算方法之一。距会计的关键定理为:
定理5.1. 给定采样概率\(q=L/n\),存在常数\(c_1\)、\(c_2\)以及算法迭代次数\(T\),对于任意的\(\epsilon<c_1q^2T\),只要:
算法 图5.2.2 对于任意的\(\delta>0\)是满足\(( \epsilon,\delta)-dp\)的。
该定理将隐私损失的上界降低到\((q \epsilon \sqrt{T},\delta)\),相比于利用基础的高斯噪声,强组合性质有了很大的提升 (Dwork et al., 2010) 。
5.2.2.3. 输出空间:差分隐私扰动目标函数¶
在输出结果上使用差分隐私机制往往会对结果产生较大的负面影响,且适用的算法很有限。因此,在输出层部署差分隐私机制的主要策略是扰动模型的目标函数而非输出结果。
Zhang等人 (Zhang et al., 2012) 在回归问题的多项式化目标函数中提出函数机制(functional mechanism),通过对每一个多项式系数添加拉普拉斯噪声,以达到扰动目标函数的目的。给定数据集\(D=\{t_1,\ldots,t_n \}\),数据样本\(t_i=( x_{i1},\ldots, x_{id}, y_i)\),回归模型的参数为\(w \in \mathbb{R}^d\),第\(j\)维的参数可表示为\(w_j\),则回归模型的最优化参数可表示为:
其中,\(\mathcal{L}\)表示损失函数。令\(\phi( w)\)表示\(( w_1, w_2,\ldots, w_d)\)的乘积,\(\phi( w)= w_1^{c_1} \cdot w_2^{c_2} \ldots w_d^{c_d}\),\(c_1,\ldots,c_d\in \mathbb{N}\)。\(\Phi_j(j\in \mathbb{N})\)则表示\(( w_1, w_2,\ldots, w_d)\)\(j\)次方的乘积:
例如\(\Phi_0=\{1\}\),\(\Phi_1 =\{ w_1,\ldots, w_d\}\),\(\Phi_2=\{ w_i \cdot w_j \ | \ i,j\in [1,d] \}\)。对于任意连续可微函数\(\mathcal{L}(t_i, w)\),根据Stone-Weierstrass理论 (Rudin and others, 1976) 其可被写成下列多项式形式:
其中,\(J\in [0,\infty]\),\(\lambda_{\phi t_i}\in \mathbb{R}\)是多项式系数。类似的,回归模型的损失函数\(\mathcal{L}_D( w)\)也可以被表示为含有\(w_1,\ldots, w_d\)的多项式形式:
回归问题的函数机制可通过算法 图5.2.3 实现。

图5.2.3 算法 函数机制(functional mechanism) (Zhang et al., 2012)¶
Phan等人 (Phan et al., 2016) 通过泰勒展开(Taylor expansion)对基于Softmax归一化层定义的交叉熵损失函数进行多项式化,并利用函数机制提出 差分隐私自编码器 模型。然后,研究者 (Phan et al., 2017) 又利用切比雪夫展开(Chebyshev expansion)将 卷积深度信念网络 (convolutional deep belief network,CDBN)的非线性目标函数进行多项式化,并在得到的多项式上添加噪声以实现差分隐私保护。
5.3. 联邦学习¶
5.3.1. 联邦学习概述¶
近年来,随着人工智能技术在各行业的落地应用,人们越来越关注其自身数据的安全和隐私,国家相关机构也出台新的法律来规范个人数据的合规使用。例如,中国于2017年开始实施的《中华人民共和国网络安全法》、2021年发布的《数据安全法》和《个人信息保护法》、欧盟于2018年开始执行的《通用数据保护条例》(General Data Protection Regulation,GDPR)等,都对用户数据的采集和使用做出了严格要求。
传统机器学习将多方数据汇集到一个中心节点,并中心节点负责使用汇集的数据进行模型训练。现实是,不同的机构之间可能出于行业竞争等因素的考虑,不愿意向其他机构共享数据,形成大量的“ 数据孤岛 ”(data silos)。此外,如果中心点遭受恶意攻击,则可能会泄露所有参与方的隐私数据。在这样的大背景下,将多方数据汇聚到中心节点统一处理的方式就会变得越来越难以实现。
学术界和工业界都在探索如何在保护各方数据安全的前提下完成多方协作训练(multi-party collaborative training)。联邦学习(federated Learning,FL)在这样的大背景下应运而生,其核心思想就是 用模型梯度(或参数)传递代替数据传递 ,可以保证在数据不出本地的前提下,多方协作完成一个全局模型的训练。谷歌在2016年将联邦学习部署于智能手机,用在手机输入法中的下一单词预测 (McMahan et al., 2017, McMahan et al., 2016) ,成为联邦学习首个成功应用的典范,为机器学习开启了一种新的范式。
联邦学习的优化目标是使各参与方的平均损失最小,可表示如下:
其中,\(N\)为参与方的个数,\(X_i\)和\(Y_i\)表示第\(i\)个参与方的本地训练样本集和标签集,\(\mathcal{L}\)为损失函数,这里假设各参与方使用相同的模型\(f_{W}\) 1。
5.3.1.1. 联邦类型¶
典型联邦学习框架是一种“参与方-服务器”结构。参与方利用本地数据更新本地模型,服务器则负责聚合不同参与方的梯度信息并完成对全局模型的更新。服务器端通常由可信第三方机构或者数据体量最大的参与方来担任。参与方上传的梯度信息中仍然包含大量参与方本地数据的隐私信息,可以使用差分隐私 (Abadi et al., 2016) 和同态加密 (Aono et al., 2017) 进行保护。经典联邦学习的架构如图 典型联邦学习框架 yang2019federated 所示。首先,参与方利用本地数据计算模型梯度,并将梯度信息进行加密后发送至服务器;然后,服务器聚合参与方的加密梯度,并将聚合后的梯度广播至各参与方;最后,参与方对收到的信息进行解密,并利用解密的梯度信息更新模型参数。
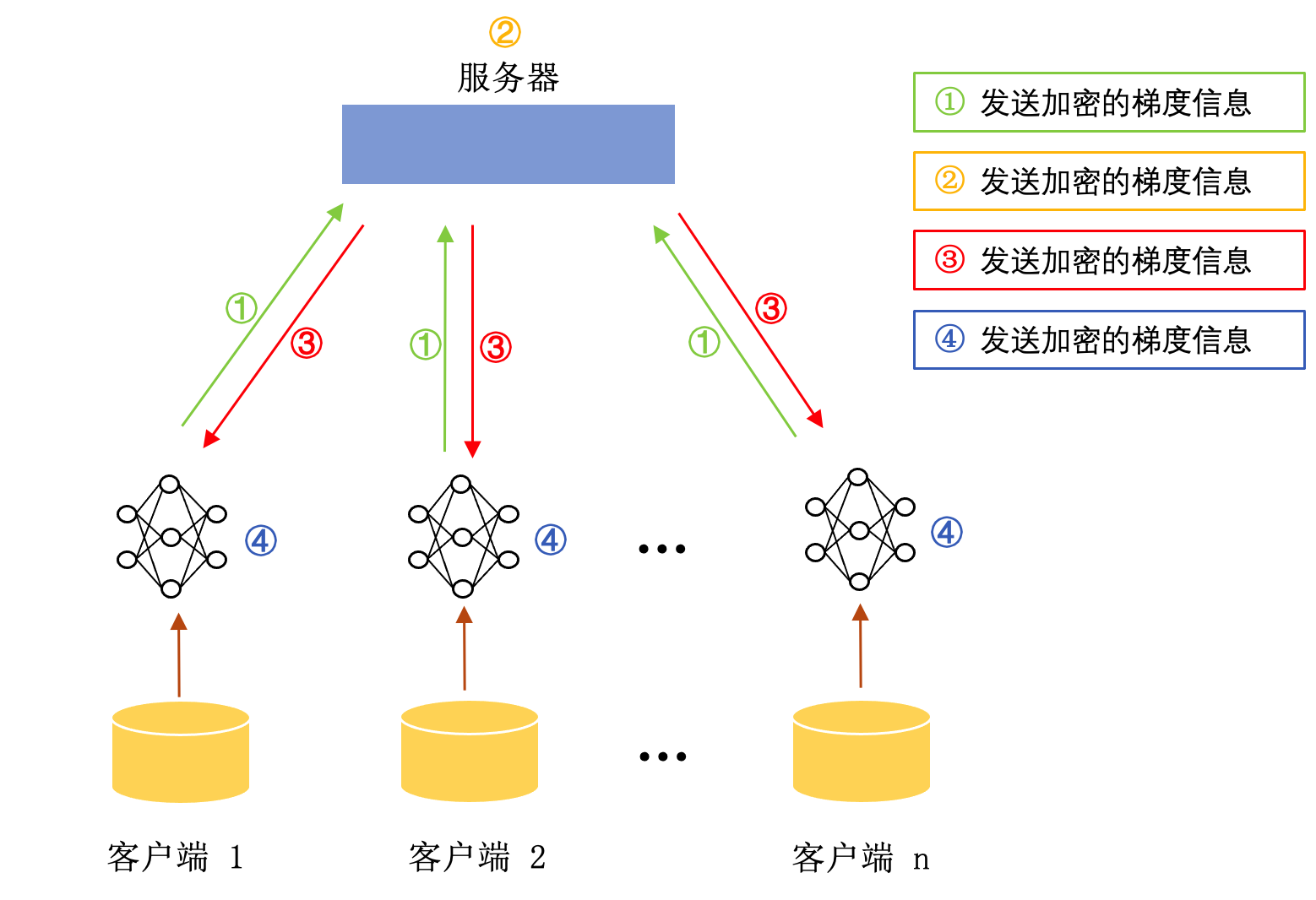
图5.3.1 典型联邦学习框架 (Yang et al., 2019)¶
在经典联邦框架下,中心服务器的可信性是人们一直讨论的一个话题。有些研究提议使用去中心化的联邦学习来代替经典联邦学习 (Yang et al., 2019) ,以摆脱对第三方机构的依赖,提高多方协作训练的可信性与安全性。 本章节将在有可信第三方中心节点的前提下,介绍经典(中心化的)的联邦学习方法,对去中心化训练框架感兴趣的同学可自行查阅相关文献学习。
联邦学习可分为横向联邦学习、纵向联邦学习和迁移联邦学习。令\(I\)为数据样本ID空间、\(X\)为样本特征空间、\(Y\)为样本标签空间,则一组训练数据集可表示为\((I,X,Y)\),参与方\(i\)的本地数据集为\(D_i = (I_i, x_i,Y_i)\)。以表格数据为例,如图 横向联邦学习 所示,横向联邦学习(horizontal federated learning, HFL),又称特征对齐的联邦学习(feature-aligned federated learning),相当于对全局数据集进行横向切分,不同的参与方拥有相同的特征集但是不同的数据样本。也就是说,横向联邦学习适用于各参与方特征重叠较多,但样本ID重叠较少的情况,多方协作的目的是增加训练样本数量。比如不同城市的银行之间通常具有类似的业务(数据特征),但是拥有不同用户(数据样本ID)。
与横向联邦学习相对,纵向联邦学习(vertical federated learning,VFL),又称样本对齐的联邦学习(sample-aligned federated learning),相当于对全局数据集进行纵向切分。再次以表格数据为例,如图 纵向联邦学习 所示,不同参与方拥有重叠的样本ID但是不同的特征集合。所以纵向联邦学习适用于各参与方之间数据样本ID重叠较多但特征重叠很少的情况,协作的目的是增加数据特征。比如同一地区的银行和电商之间拥有相同的客户群体,但是不同的业务和数据特征。
在迁移联邦学习(transfer federated learning,TFL)下,各参与方之间即缺少共有客户(数据样本ID),也没有(或者很少)重合特征,比如不同城市的银行和电商之间业务特征和用户群体都没有交集。图 迁移联邦学习 展示了基于表格数据的迁移联邦学习各参与方的数据拥有情况。
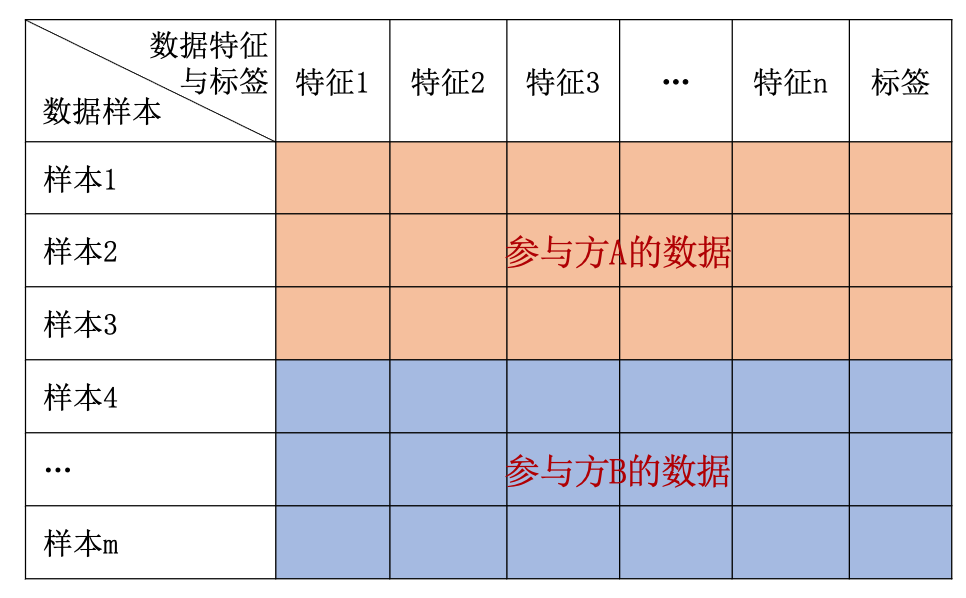
图5.3.2 横向联邦学习¶
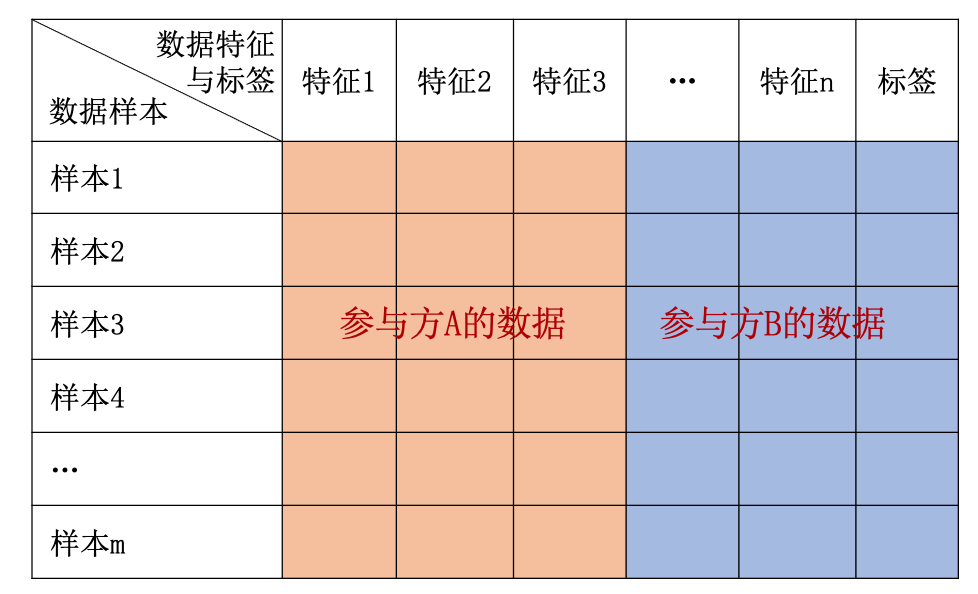
图5.3.3 纵向联邦学习¶

图5.3.4 迁移联邦学习¶
从2016年提出至今,联邦学习得到了学术界和工业界的广泛关注,先后提出了很多联邦学习的开源框架。 图5.3.5 统计了几个具有代表性的开源框架,包括开发者信息、是否支持横/纵向联邦以及支持的加密算法等。
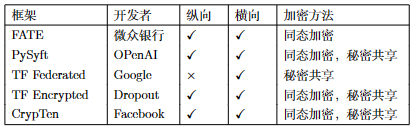
图5.3.5 联邦学习框架¶
5.3.1.2. 同态加密¶
联邦学习机制的提出让各参与方在本地数据不外泄的前提下完成全局模型的训练,然而参与方向外传输的梯度信息仍然可能包含有关训练数据的敏感信息,导致恶意参与方可以通过梯度反推出其他参与者的隐私信息。这可以通过同态加密(homomorphic encryption,HE)来有效解决,同态加密通过实现数据的“可算不可见”有效保护参与方的梯度信息安全。同态加密是密码学的经典问题,Rivest等人 (Rivest et al., 1978) 于1978年首次提出同态加密的概念:数据经过加密之后,对密文进行一定计算,后将密文的计算结果进行解密的过程,等同于直接对明文数据进行对应计算。
同态加密可表示为一个四元组\(H=\{ KeyGen, Enc,Dec,Eval \}\)。其中\(KeyGen\)为密匙生成函数,\(Enc\)为加密函数,\(Dec\)为解密函数,\(Eval\)为评估函数。加密的方式有 对称加密 和 非对称加密 两种。令\(M\)为明文空间,\(C\)为密文空间,对于对称加密来说,首先由密匙生成元\(g\)和密匙生成函数\(KeyGen\)生成密钥\(sk=KeyGen(g)\),然后使用加密函数\(Enc\)对明文\(M\)进行加密\(C=Enc_{sk}(M)\),解密则使用\(Dec\)对密文\(C\)进行解密\(M=Dec_{sk}(C)\)。对于非对称加密,使用密匙生成元\(g\)和密匙生成函数\(KeyGen\)生成\((pk,sk)=KeyGen(g)\),其中\(pk\)为公匙,用于对明文加密\(C=Enc_{pk}(M)\),\(sk\)为私匙,用于对密文解密\(M=Dec_{sk}(C)\)。
以对称加密为例,满足以下条件的加密系统称为同态:
其中,\(f_M\)为明文空间的运算函数,\(f_C\)为密文空间的运算函数,\(\gets\)表示右边项等于左边项或者右边项可直接计算出左边项。上式条件是指在密文上运算与直接在明文上运算再加密是等价的。
同态加密又可分为三类:半同态加密(partially homomorphic encryption,PHE)、部分同态加密(somewhat homomorphic encryption,SWHE)和全同态加密(fully homomorphic encryption,FHE)。半同态加密是指只支持加法或乘法中的一种运算,支持加法运算的又称为加法同态加密(additive homomorphic encryption,AHE),如RSA、GM (Shafi and Silvio, 1982) 等;部分同态加密可同时支持加法和乘法运算,但支持的计算次数有限,如BGN (Boneh et al., 2005) 等;全同态加密则可支持任意次数的加法和乘法运算。Gentry (Gentry, 2009) 于2009年首次实现全同态加密,轰动了学术界,激发了学者对全同态的研究热情,也因此诞生了诸多优秀的全同态加密算法,如BFV (Fan and Vercauteren, 2012) 、BGV (Brakerski et al., 2014) 等。
5.3.2. 横向联邦¶
如前文所述,横向联邦学习中各参与方的特征重叠而样本不重叠,从全局数据集的角度来看构成了一种横向切分的效果。 横向联邦的适用场景非常广泛,除了可以解决同类业务不同地域之间的数据孤岛问题,也可以联合数量庞大的移动设备,如智能手机、智能电器、无人机等,训练一个强大的全局模型。当参与设备为智能手机等算力较弱的设备时,参与方与服务器之间的梯度信息传输代价将高于其计算代价。因此,联邦学习通常不使用随机梯度下降来更新全局模型,而是使用联邦平均(FedAvg) (McMahan et al., 2017) ,让参与方在本地数据上多进行几次迭代后,再将梯度信息(或模型参数)传输到服务器端进行平均和更新,具体步骤如算法 图5.3.6 所示。

图5.3.6 联邦平均(FedAvg)¶
FedAvg算法虽然通过参与方在本地的多次迭代,减少了通信的代价,但是迭代次数过多也会增加参与方节点的算力负担,甚至会使一些算力受限的参与方无法完成训练,同时多次迭代也会使参与方的本地模型偏离全局模型,进而影响全局模型的收敛。导致这一问题的根本原因在于联邦学习中的异质性(heterogeneity),包括各参与方之间的设备异质、数据异质和模型异质等等。设备异质会使得设备间的通信和计算存在较大差异,导致不同设备之间更新不同步等问题;数据异质主要是由于不用参与方的个性化使得数据非独立同分布(non-independently and identically distributed,Non-IID);而模型异质是由于计算资源的限制导致不同设备可能会选择不同(量级)的模型来参与运算。
FedProx算法 (Li et al., 2020) 则从异质性入手对FedAvg做了两点改良。首先,与FedAvg在每轮迭代中让各参与方进行相同周期(epoch)的本地训练不同,FedProx允许参与方根据自身算力进行不同周期的本地训练。其次,FedProx在参与方的目标函数里增加了近端项(proximal term),以加速全局模型的收敛:
其中,\(\mathcal{L}(f(X_i),Y_i)\)为参与方\(i\)原始的损失函数,\(\frac{\mu}{2}\|W_t-W_t^i \|\)为其增加的近端项,\(W_t\)为\(t\)时刻的全局模型,\(W_t^i\)为参与方当前求解的本地模型。其他类似的算法,如SCAFFOLD算法 (Karimireddy et al., 2020) 和PFedMe算法 (T Dinh et al., 2020) 与FedProx的思想一致,但是正则化方式不同,比如SCAFFOLD采用全局模型来约束修正参与方本地模型的训练,而PFedMe则结合Moreau Envelope光滑化进行近端项的正则化。
经典的联邦学习是联合多个参与方,协同训练出一个全局模型,但是由于数据的异质性,一个全局模型很难对每个参与方都适用。对此,Jiang等人 (Jiang et al., 2019) 提出了个性化联邦学习(personalized FL,PFL)的概念,采用模型不可知的元学习(model agnostic meta learning,MAML)思路,将FedAvg解释为一种元学习算法,除了参与方协同训练的全局模型外,还有各自的个性化模型。具体来说,研究者提出Personalized FedAvg算法,先使用FedAvg得到初始模型,其中参与方采用较大的迭代周期;然后,对FedAvg得到的初始模型进行微调;最后在参与方本地进行个性化操作。其他相关的方法,如Per-FedAvg (Fallah et al., 2020) 和FedMeta (Chen et al., 2018) ,也都是在FedAvg的框架下利用元学习思想对本地训练和全局更新部分进行调整。
除了元学习,多任务学习也成为解决联邦学习个性化的新方法。在 (Smith et al., 2017) 和 (Vanhaesebrouck et al., 2017) 这两个相对早期的工作中,研究者将联邦学习的个性化定义为一个多任务问题,将参与方之间的关系定义为惩罚项,进而通过优化惩罚项进行个性化学习。聚类联邦学习(clustered FL,CFL) (Sattler et al., 2020) 则进一步结合多任务和聚类思想解决数据异质所导致的局部最优问题,在训练的过程中将模型参数相近的参与方分为一组,同一组的参与方进行知识共享,以此完成联邦学习的个性化。
更进一步,FedEM算法 (Marfoq et al., 2021) 从参与方的数据分布着手,做了两点假设:一是参与方数据为\(M\)个未知的潜在分布的混合,让每个参与方的模型由\(M\)个子模型集成得到;二是针对混合分布利用期望最大(expectation maximization, EM)算法优化。每个参与方的个性化则通过赋予\(M\)个子模型不同的权重完成,前期的个性化联邦学习方法,包括聚类 (Sattler et al., 2020) 、多任务 (Smith et al., 2017) 以及模型插值 (Deng et al., 2020) 等,都可以被理解为是该算法的特例。
5.3.3. 纵向联邦¶
在纵向联邦学习中,参与方拥有的特征不同但是样本ID重叠较多,适用于同地域内不同行业之间的协作训练。比如在银行与电商场景下,银行拥有当地用户的经济收支、借贷以及信用等级等信息,而电商平台则拥有用户的购买记录,在一定程度上可以反映用户的消费习惯和产品偏好,这两家机构的联合可以训练出特征更全、性能更优的模型,比如理财产品推荐模型。类似的联邦还可以发生在更多的行业之间,如医疗、保险、房地产、娱乐、教育等。 纵向联邦学习主要包含两个步骤,首先是不同机构之间相同实体的对齐,其次便是利用共同用户实体的数据协同训练模型 (Yang et al., 2019) 。本节将展开介绍两个经典的纵向联邦学习算法。
安全线性回归(secure linear regression,SLR) (Yang et al., 2019) 可以说是最常用、最经典的纵向联邦学习算法,是线性回归算法的联邦化版本,所以也称联邦线性回归。安全线性回归之所以称为“安全”是因为它使用同态加密技术保护参与方之间传输信息的安全。
假定有A、B两个参与方,其中只有B方拥有数据的标签,即A方数据为\(\{ x_i^A\}_{i=1}^{n_A}\),B方数据为\(\{ x_i^B,y_i\}_{i=1}^{n_B}\),其中\(x_i^A, x_i^B\)为数据特征,\(y_i\)为数据标签。令\(w_A, w_B\)为A、B双方的模型参数,则安全线性回归的优化目标为:
简化起见,令\(u_i^A= w_A x_i^A\),\(u_i^B= w_B x_i^B\),\([[\cdot]]\)表示加法同态加密,则加密后的目标函数可表示为:
利用加法同态的性质,令\([[\mathcal{L}_A]]=[[\sum_i( u_i^A)^2+\frac{\lambda}{2}\| w_A\|^2 ]]\),\([[\mathcal{L}_B]]=[[\sum_i( u_i^B-y_i)^2+\frac{\lambda}{2}\| w_B\|^2 ]]\),\([[s_{AB}]]=2\sum_i [[ u_i^A( u_i^B-y_i) ]]\)。则式 (5.3.5) 可表示为:
在使用梯度下降算法进行模型优化时,A、B双方的梯度分别为:
其中,\([[d_i]]=[[ u_i^A]]+[[ u_i^B-y_i]]\)。由此可见,A、B双方为了求得准确的梯度,均需要对方的信息。此外,为了防止A、B双方通过传输的信息窥探对方的隐私信息,需要借助一个安全可信的第三方来协助完成加密解密工作。这里的第三方可以选择公信力和权威性较高的机构,如政府机构、学术组织等。综上,安全线性回归的完整步骤如表 图5.3.7 所列。在完成模型训练之后的推理阶段,仍需A、B双方在第三方的协助下完成,步骤见表 图5.3.8 。
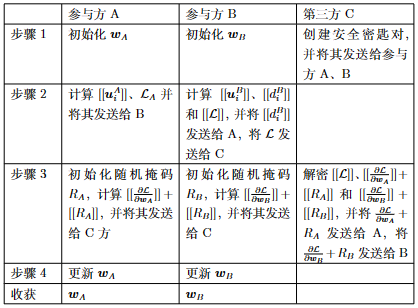
图5.3.7 安全线性回归算法的训练步骤¶
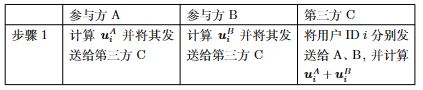
图5.3.8 安全线性回归算法的预测步骤¶
安全提升树(SecureBoost) (Cheng et al., 2021) 是第二个常用且经典的纵向联邦学习算法。安全提升树是XGBoost的联邦化版本,本节先介绍XGBoost算法,然后再介绍如何将其联邦化得到安全提升树。
给定一个拥有\(n\)个样本和\(d\)个特征的数据集\(X \subset \mathbb{R}^{n\times d}\),XGBoost算法通过集成\(K\)个回归树\(f_k\)完成预测任务:
XGBoost通过迭代寻找一组回归树,使得集成后的预测标签与真实标签之间的距离最小。不失一般性,XGBoost第\(t\)轮的优化目标可定义为:
其中,\(\Omega(f_t)=\gamma T+\frac{1}{2}\lambda\|w\|^2\)计算树的复杂度,\(g_i =\partial_{\hat{y}^{(t-1)}}\mathcal{L}(\hat{y}^{t-1},y_i)\)和\(h_i =\partial_{\hat{y}^{(t-1)}}^2\mathcal{L}(\hat{y}^{t-1},y_i)\)。
在第\(t\)次迭代中,回归树的构建都是从深度为0开始,然后在每个节点分割,直到达到最大深度为止。节点的最佳分割可使用下式进行计算:
其中,\(I_L\),\(I_R\)分别代表分割后左右子节点的样本空间。在得到最佳分割点后,便要决定叶节点\(j\)的最佳权重,计算公示为:
其中,\(I_j\)为叶节点\(j\)的样本空间。
上述内容是XGBoost算法的关键信息,但传统XGBoost是将所有数据收集在一起进行模型训练的,而安全提升树要解决的问题就是如何让用户的数据都保留在本地的前提下,完成模型的协同训练。安全提升树将用户分为两类,一类是主动方(active party),其同时拥有数据特征和标签,可担当服务器节点;另一类是被动方(passive party),只拥有数据的特征。由式 (5.3.11) 和式 (5.3.12) 可知,回归树的最佳分割点和最佳权重值均依赖于\(g_i\)和\(h_i\)。但是如果参与方直接交换\(g_i\)和\(h_i\)则会泄露隐私信息,因为\(g_i\)和\(h_i\)的计算都依赖于样本的标签信息,被动方可基于导数以及第\(t-1\)轮的预测标签\(\hat{y}_i^{(t-1)}\)反推出原始标签信息\(y_i\)。因此双方在传递之前,对其进行同态加密保护。
然而,被动方无法在信息加密的情况下计算式 (5.3.11) ,因此分割点的评估将由主动方执行。在计算最佳分割点之前,首先被动方使用算法 图5.3.9 聚合加密梯度信息,并将其发送给主动方,然后主动方根据收到的信息计算全局最优分割点,如算法 图5.3.10 所示,使用[参与方ID(\(i_{\text{opt}}\)),特性ID(\(k_{\text{opt}}\)),阈值ID(\(v_{\text{opt}}\))]表示最佳分割。
模型训练完成后便是对新样本的预测,因为样本的真实标签只存在于主动方,因此对新样本的预测也将在主动方的主导下完成。

图5.3.9 聚合梯度统计值 (Cheng et al., 2021)¶

图5.3.10 寻找最优分割 (Cheng et al., 2021)¶
5.3.4. 隐私与安全¶
联邦学习在参与方不分享本地数据的前提下完成对全局模型的联合训练,这有效保护了参与方的数据隐私。然而,联邦学习也面临新的隐私和安全问题,例如在参与方-服务器架构中,恶意服务器可能会利用参与方上传的梯度信息反推其隐私信息,或者在训练过程中篡改相关信息;恶意参与方可能会窥探其他参与方的隐私信息,或者通过向服务器发送恶意梯度信息破坏全局模型。本节将介绍联邦学习所面临的两大主要安全隐患(隐私攻击和投毒攻击)以及防御措施。
5.3.4.1. 隐私攻击与防御¶
梯度信息是联邦学习过程中所交换的一类主要信息,梯度虽然不等同于原始数据,但是依然会泄露参与方的部分信息。而至于梯度到底会泄漏多少隐私信息,目前并未有确切的结论。在联邦学习中,虽然梯度是在参与方的本地数据上计算得到的,但是全局模型的训练可以看作是对所有参与方数据的高度统计 (Lyu et al., 2022) 。对深度学习模型来说,特定层的梯度是由前层传递的特征和后层传递的误差计算得到的,因此梯度信息可以被用来反推众多的隐私信息,比如某类别的典型样本以及训练数据的成员和属性等,更甚至是逆向出原始训练数据 (Zhu et al., 2019) 。此外,大部分针对传统机器学习的攻击方法也适用于联邦学习,例如对抗攻击可以直接攻击全局模型,进而攻击所有参与方;后门攻击可以通过攻击单个本地模型来间接攻击全局模型;成员推理攻击既可以攻击单个模型(基于其上传的梯度)也可以攻击全局模型。
隐私攻击主要是推理类型的攻击,可分为四种,分别推理典型样本、成员、属性和训练数据。针对单个机器学习模型的隐私攻击请参阅章节 4.2节 ,这里主要介绍对联邦学习的攻击。
典型样本推理。Hitaj等人 (Hitaj et al., 2017) 设计了首个针对联邦学习的隐私攻击方法,该方法使用生成对抗网络推理其他参与方的典型样本(prototypical samples)信息。假设受害者拥有的数据标签为\([a,b]\),攻击者拥有的数据标签为\([b,c]\),攻击者的目标是在联邦学习过程中本地训练一个生成对抗网络来生成类别\([a]\)的样本。由于全局模型是共享的,所以攻击者可以知道所有的类别,并且可以使用全局模型作为生成对抗网络的判别器。在每轮训练中,攻击者利用具有类别\([a]\)的判别器,训练生成器生成\([a]\)类别的样本,并将生成的样本标记成\([c]\)类别进行本地训练。此时,由于类别\([a]\)的生成数据被标记成了类别\([c]\),所以受害者会在下一轮的本地训练中,不知不觉的增强对\([a]\)类别样本的学习和修正,导致泄露更多关于\([a]\)类别的样本信息。攻击者以此迭代,可以训练一个生成器生成类别\([a]\)的典型样本(跟原始样本不完全相同但是来自于同一分布)。
成员推理。针对联邦学习的成员推理攻击旨在推理某个样本是否出现在其他参与方的训练数据集中,可分为主动推理和被动推理两类。被动推理攻击只观察全局模型的参数信息但不改变联邦学习的训练协议,而主动推理攻击则可篡改训练过程中上传的梯度信息以构造更强大的攻击 (Melis et al., 2019, Nasr et al., 2019) 。深度学习模型在非数字数据(比如文本)上进行训练时,其输入空间往往是离散且稀疏的,这时候需要先用嵌入层(embedding layer)将输入变成一个低维向量表示。在自然语言处理模型中,嵌入层的梯度往往是稀疏的(出现某个单词的地方不为零,其他地方都是零),所以被动推理攻击者可以根据嵌入层的梯度信息反推出哪些单词在当前的训练数据集中 (Melis et al., 2019) 。主动推理攻击的代表方法是梯度上升(gradient ascent) (Nasr et al., 2019) ,攻击者将目标数据所产生的梯度增大,如果目标数据在其他参与方的训练集中,则在后续的训练过程中该部分的梯度会得到大幅的减小,否则下降幅度则比较温和,以此完成成员推理攻击。
属性推理。属性推理也可分为主动和被动两种方式 (Melis et al., 2019) 。被动属性推理往往先借助辅助数据(auxiliary data),基于当前的模型快照(snapshots)在辅助数据上生成含有目标属性的模型更新和不含目标属性的模型更新。如此得到的两类模型更新便组成了一个二分类数据集,可以用来训练一个二分类器。在联邦学习过程中,攻击者可以使用训练的二分类器,根据全局模型的更新判断是否存在对应的属性。而主动属性推理则是借助多任务学习(multi-task learning),将目标属性的识别任务和主任务进行结合训练出一个增强分类器。训练所使用的损失函数可定义为:
其中,\(y\)为主任务标签,\(p\)为属性任务标签,\(W\)为模型参数。主动推理和被动推理的主要区别在于主动推理进行了额外的计算,而且额外计算的结果参与到了全局模型的训练过程之中。
训练数据窃取。 Zhu等人 (Zhu et al., 2019) 提出深度梯度泄露(deep leakage from gradients,DLG)攻击,揭示协作学习过程中梯度的交换会泄露训练数据的问题,严重时甚至可以在像素级别(pixel-wise)和词元级别(token-wise)还原原始训练图像或文本。深度梯度泄露攻击首先随机生成一份与真实样本大小一致的虚拟样本和虚拟标签,并初始化一个机器学习模型,然后利用虚拟样本和虚拟标签计算虚拟梯度,通过优化虚拟梯度与真实梯度之间的距离,让虚拟输入逼近真实输入。其优化目标函数为:
其中,\(x'\)和\(y'\)分别为虚拟样本和虚拟标签,\(W\)为攻击者训练的模型参数,\(\nabla_{W'}\mathcal{L}\)和\(\nabla_{W}\mathcal{L}\)分别表示虚拟梯度和真实梯度。
隐私防御方法主要有三种。首先是同态加密,各参与方在上传梯度前先对其进行加密,上传密文而不是明文。同态加密的基本概念在章节中 图5.3.5 已介绍,这里不再赘述。虽然同态加密可以很好的保护梯度安全,但是会增加计算和存储负担,对算力较小的参与方并不适用。其次是多方安全计算(secure multiparty computation,SMC) (Yao, 1982) ,它可以在不依赖可信第三方的情况下,让多个参与方不透露隐私信息且合作计算任意函数。多方安全计算的协议都涉及到一些基本的构造块,如不经意传输(oblivious transfer,OT)、零知识证明(zero-knowledge proof,ZKP)、混淆电路(garbled circuit,GC) 2 等,这些构造块为多方安全计算的理论和实践奠定了基础。安全机器学习(secure machine learning)将多方安全计算引入机器学习,保护其训练过程的隐私,为多种模型,如线性回归、逻辑回归和神经网络等,设计了安全协议。但是多方安全计算往往以高算力和高通信开销为代价来换取隐私保护,成为其实际应用的主要障碍。最后是差分隐私,其通过向原始数据或者模型参数中添加随机噪声来保护数据隐私,相关概念也已在章节 5.2节 中介绍,这里也不再赘述。
5.3.4.2. 投毒攻击与防御¶
在隐私攻击中,攻击者意在窥探其他参与者的隐私数据,而投毒攻击的目的则是降低全局模型的性能、鲁棒性或者操纵全局模型。针对联邦学习的投毒攻击大致可以分为两类,一是无目标攻击 (Jagielski et al., 2018, Rubinstein et al., 2009) ;二是有目标攻击 (Bagdasaryan et al., 2020, Shafahi et al., 2018) 。需要注意的是,针对联邦学习的投毒攻击是一个很热门的研究课题,新型威胁模型和攻击算法层出不穷。
无目标攻击。无目标攻击的目的是破坏全局模型的完整性,使全局模型无法收敛。拜占庭攻击(Byzantine attack)就是无目标攻击的一种。在联邦学习中,一个诚实的参与方\(i\)向服务器传输的更新信息为\(\bigtriangleup w_i=\nabla_{ w_i} \mathcal{L}(f_i( x),y)\),而拜占庭参与方可以根据自己的意图向服务器发送任何恶意信息,比如下式定义的“任意”梯度:
其中,\(*\)为任意值,\(f_i\)为参与方\(i\)的本地模型,\(w_i \in \mathbb{R}^m\)为\(f_i\)的参数。
研究表明,即使只有一个参与方发动拜占庭攻击,全局模型也会被轻易的控制 (Blanchard et al., 2017) 。假如联邦学习系统中有\(n\)个参与方,其中前\(n-1\)个为诚实参与方,第\(n\)个为拜占庭参与方,服务器聚合参与方的更新梯度为\(\bigtriangleup w'=\sum_{i=1}^n \bigtriangleup w_i\)。若拜占庭参与方的攻击目标是使服务器聚合后的梯度为\(u\),则其向服务器传输的梯度可设置为\(\bigtriangleup w_n=n u-\sum_{i=1}^{n-1} \bigtriangleup w_i\)。 其他拜占庭攻击的方式还有:(1)高斯噪声攻击,\(\bigtriangleup w_i=\bigtriangleup w_i+\mathcal{N}(0,\sigma^2)\),\(\mathcal{N}(0,\sigma^2)\)为高斯分布;(2)相同值攻击,\(\bigtriangleup w_i=c\mathbf{1}\),\(\mathbf{1}\)为全1矩阵;(3)符号反转攻击,\(\bigtriangleup w_i=c w_i\)(\(c<0\))。
防御无目标攻击。 针对拜占庭攻击的防御目前主要是从容错性(fault tolerance)的角度考虑,提升服务器端梯度聚合算法的鲁棒性。以经典的鲁棒聚合算法Krum (Blanchard et al., 2017) 为例,其出发点是计算单个参与方梯度与其他参与方梯度的距离和,将距离和较远的参与方判定为潜在的拜占庭攻击者,在服务器梯度聚合时将其剔除,不纳入计算。假设联邦学习系统中有\(n\)个参与方,在第\(t\)轮迭代的梯度更新为\(\{\bigtriangleup w_1^t,\bigtriangleup w_2^t,\ldots,\bigtriangleup w_n^t \}\),其中假设\(b\)个为拜占庭参与方。服务器在收到参与方的梯度信息后,计算\(w_i^t\)的\(n-b-2\)近邻集合\(C_i\),并利用它们之间的距离计算一个分数:
最后服务器利用得分最低的梯度信息\(w_{\text{Krum}}= w_i^t\)更新全局模型\(W^{t+1}=W^t+ w_{\text{Krum}}\)。理论上,Krum最多可以防御的拜占庭攻击者的个数\(b\)是有限制的,即\(n>2b+3\)。
巧妙的利用均值、中位数等统计知识来代替个别参与方的异常梯度也是防御拜占庭攻击的重要方法。Yin等人 (Yin et al., 2018) 提出坐标中值(coordinate-wise median)和坐标截尾均值(coordinate-wise trimmed mean)聚合方法,使用参与方上传梯度的中位数或截尾均值来完成鲁棒聚合。已知\(\bigtriangleup w_i \in \mathbb{R}^m\),则坐标中值聚合的梯度为:
它的第\(k\)维计算公式为:\(g_k=\text{median}(\{\bigtriangleup w_i^k,i\in[n] \})\),其中\(\bigtriangleup w_i^k\)为\(\bigtriangleup w_i\)的第\(k\)维信息。使用坐标截尾均值聚合的梯度为:
第\(k\)维计算公式为:\(g_k=\frac{1}{1-2\beta}n\sum_{w\in{U_k}}w\),其中\(U_k\)是由集合\(\{\bigtriangleup{w_1^k},\ldots,\bigtriangleup{w_n^k}\}\)去掉最大最小的\(\beta\)部分而得到的。类似的方法还有Bulyan (Guerraoui et al., 2018) 、RFA (Pillutla et al., 2019) 和AUROR (Shen et al., 2016) 等。
有目标攻击。 在有目标攻击中,攻击者的目的不再是破坏模型的完整性,而是想要在测试阶段控制全局模型,使其将特定样本预测为指定的标签,例如将垃圾邮件预测为非垃圾邮件。有目标攻击的难度通常要高于无目标攻击,其攻击策略主要有两大类:一类是标签翻转(label flipping) (Biggio et al., 2012) ,攻击者将一类样本的标签改为其他类别;另一类则是后门攻击 (Bagdasaryan et al., 2020) ,攻击者修改原始样本的个别特征或者较小的区域以达到攻击的目的。标签翻转的实施较为简单,但是隐蔽性差,因为其很容易在验证集上检测出来,相比之下后门攻击更加隐蔽,因为它只是向模型中注入额外的触发器但不影响模型的常规性能。目前,针对联邦学习的有目标攻击大都通过后门攻击来完成,而且针对传统单机器学习模型设计的大量后门攻击可以快速的迁移到联邦学习中来。 后门攻击的实施又分为两种情况:一是攻击者可以改变样本的标签(也就是结合了标签翻转攻击) (Gu et al., 2017) ,二是攻击者不改变标签信息(即干净标签攻击) (Muñoz-González et al., 2017) ,这样的攻击也更隐蔽。实际上,联邦学习更易受后门攻击,因为其联合训练的范式很容易将某个参与方的后门传染到全局模型,继而影响到所有的参与方。这些攻击将会在章节 8节 进行详细的介绍。
防御有目标攻击。 传统机器学习范式下的后门防御策略,如后门检测和后门移除等,将在章节 9节 中进行介绍,这里不再赘述。 在联邦学习方面,Sun等人 (Sun et al., 2019) 提出使用范数约束(norm thresholding)来防御后门攻击。因为攻击者上传的梯度可能具有较大的范数,所以服务器可以将范数超过一定阈值\(M\)的梯度视为潜在的后门攻击。对此,范数约束通过下列方式完成鲁棒梯度聚合:
其中,\(W_{t+1}\)为第\(t+1\)轮迭代中服务器端聚合的参与方梯度,\(S_t\)为参与此次更新的参与方集合。该方法可以确保每个参与方的梯度更新都比较小,从而可以最大限度的减少其对全局模型的影响。当然,一旦攻击者知道服务器端所设定的阈值\(M\),那么其可以将攻击梯度的范数限制在阈值之内,让基于范数的防御失效。 此外,还可以通过权重剪枝 (Wu et al., 2020) 和参数平滑 (Xie et al., 2021) 的方法来防御联邦学习中的后门攻击。
我们将现有防御方法在表 图5.3.11 中进行了一定的总结。我们将这些方法进行了属性概括,分为核心技术、是否适用于独立同分布(IID)和非独立同分布(Non-IID)的环境、可防御的最大攻击者数量(即断点)、以及是否可以防御有目标攻击和无目标攻击等。
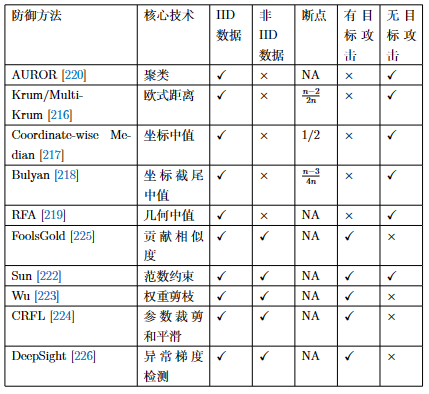
图5.3.11 投毒攻击防御方法 (Lyu et al., 2022)¶
5.4. 篡改与深伪检测¶
媒体数据的篡改和检测正如矛与盾,二者在相互对抗的同时也在相互促进发展。上一章 4.4节 中我们介绍了媒体内容的篡改技术,本章节将介绍与其对应的防御手段——篡改检测。篡改检测可以从特征、语义等维度判断媒体数据是否被篡改过。根据被检测的媒体内容不同,检测方法主要可以分为两类:通用篡改检测和深度伪造检测。通用篡改检测主要是指检测图像中的普通物体是否被篡改,而深度伪造检测则只关心图像中的人脸部分是否被篡改。很多检测方法将这类任务看作是一类二分类任务,根据输入的图片或视频给出一个0或1的检测结果,代表输入内容是真实的(或伪造的),当然也有一些方法可以输出一个二进制的掩码(mask)来对篡改区域进行定位。
5.4.1. 通用篡改检测¶
尽管篡改方式十分多样,但现有的通用篡改检测方法主要关注这三种:拼接(splicing)、复制-移动(copy-move)和消除(removal)。拼接和复制-移动都是在目标图像上添加内容,区别在于拼接的内容往往来源于不同的图像,而复制-移动则就在目标图像中取材。消除是指将图像的某一个区域移除,然后利用背景信息进行填充。用于通用篡改检测的数据集除了提供二进制标签以外,往往还提供表示篡改区域的掩码。
早期的通用篡改检测方法可以分为两种:一种是利用相机成像过程中引入的像素间的相关性来进行分析,图像篡改往往会破坏这些相关性。例如,横向色差(lateral chromatic aberration,LCA)是由于不同波长的光在镜头玻璃中的折射角度不同而在相机传感器上产生的颜色条纹,通过分析这些特征可以判断图像是否被篡改,但横向色差可以被后期算法消除,可能使相应的检测方法失效。相机成像过程中的去马赛克算法将相机传感器输出的不完整颜色图像补全为完整的彩色图像,同样使同一区域内的像素具有了相关性。当相机使用JPEG有损压缩格式来保存图像时,会在图像上留下压缩痕迹,当图像被篡改时也会破坏这些痕迹的完整性,从而可以用来检测篡改。
此外,还可以利用图像(及其所含噪声)的频域特征或统计特征进行检测,比较有代表性的是图像非均匀响应噪声(photo-response nonuniformity noise,PRNU)。图像非均匀响应噪声可以视为相机传感器的指纹,Lukáš等人 (Lukáš et al., 2006) 提出可以通过比较相机传感器PRNU和待检测图像的PRNU之间的差异来检测图像篡改。Wang等人 (Wang et al., 2014) 利用DCT(discrete cosine transform)系数的概率分布来分析图像中的篡改痕迹。Fridrich等人 (Fridrich and Kodovsky, 2012) 提出利用图像中自然存在的噪声特征来检测篡改痕迹。Pan等人 (Pan et al., 2012) 利用局部区域的噪声方差来分析图像的篡改痕迹。这种利用噪声分布来检测异常区域的思想后续也被应用到图像修复检测 (Li et al., 2021) 和深度伪造检测。
后来的检测方法大都基于深度学习模型(比如卷积神经网络)进行,得到的检测精度和鲁棒性往往要比上述传统检测方法更优。比如,Chen等人 (Chen et al., 2015) 将中值滤波器与卷积神经网络结合,先对图像进行中值滤波处理,再送入卷积神经网络,以此来提升图像篡改检测的精度。RGB-N(RGB features for region proposal network) (Zhou et al., 2018) 检测方法则是从网络结构入手,提出了一种基于Faster R-CNN的双流网络(two-steam network)来精准定位篡改区域:RGB数据流和噪声流。具体的,RGB-N通过RGB数据流从RGB图像中提取图像特征,帮助发现强烈对比差异与不自然的篡改边界;通过噪声流从模型过滤器层中提取噪声特征,帮助识别真实区域和被篡改区域之间的噪声不一致性;最后,通过双线性汇集层将两个数据流的特征融合在一起,并进一步结合空间特征进行篡改区域的定位。实验表明,这种双流结构相比基于单流的检测在精度方面有较大提升。
Hu等人 (Hu et al., 2020) 在2020年提出了空间金字塔注意力网络(spatial pyramid attention network,SPAN),其利用堆叠的卷积层来提取图像特征,然后利用金字塔结构的局部自注意力块来模拟多个尺度上的图像块(patch)之间的关系,从而发现不同尺度图像块之间的不一致性,定位到被篡改的图像块。2021年,Liu等人 (Liu et al., 2022) 提出了PSCC-Net(progressive spatio-channel correlation network),其使用一个自上而下的路径来提取局部和全局特征,同时使用一个自下而上的路径来检测输入图像是否被篡改,并定位篡改区域。它在四种不同尺度上估计篡改掩码(manipulation mask),其中每个掩码以前一个掩码做为条件。与传统的编码器-解码器和无池结构不同,PSCC-Net充分利用不同尺度的特征和密集的交叉联系,以从粗粒度到细粒度的方式产生篡改掩码。此外,PSCC-Net使用一个空间-通道相关模块(spatio-channel correlation module,SCCM)在自下而上的路径中捕捉空间和通道的相关性,从而获取更多全局线索,应对更广泛的篡改手段。此外,在篡改定位方面,如何摒弃耗时的预处理和后处理操作,实现端到端的训练也是一个挑战。对此,Mantra-Net (Wu et al., 2019) 将定位篡改区域的问题表述为一个局部异常检测问题,设计Z-score特征来捕捉局部异常,提出一个新的长短期记忆模块(long short-term memory),并结合自监督训练来检测和定位篡改区域。ManTra-Net是一个端到端的纯卷积网络,可以检测任何大小的图像,灵活应对多达385种不同的图像篡改类型。
5.4.2. 深度伪造检测¶
与通用篡改相比,篡改了人脸的媒体内容更容易传播,更容易对现实社会产生影响,所以亟需能够高效应对人脸深度伪造的检测方法。现有深度伪造检测技术(主要是视觉方面)可以简单分为图片检测与视频检测。更详细的分类如图 图5.4.1 所示。
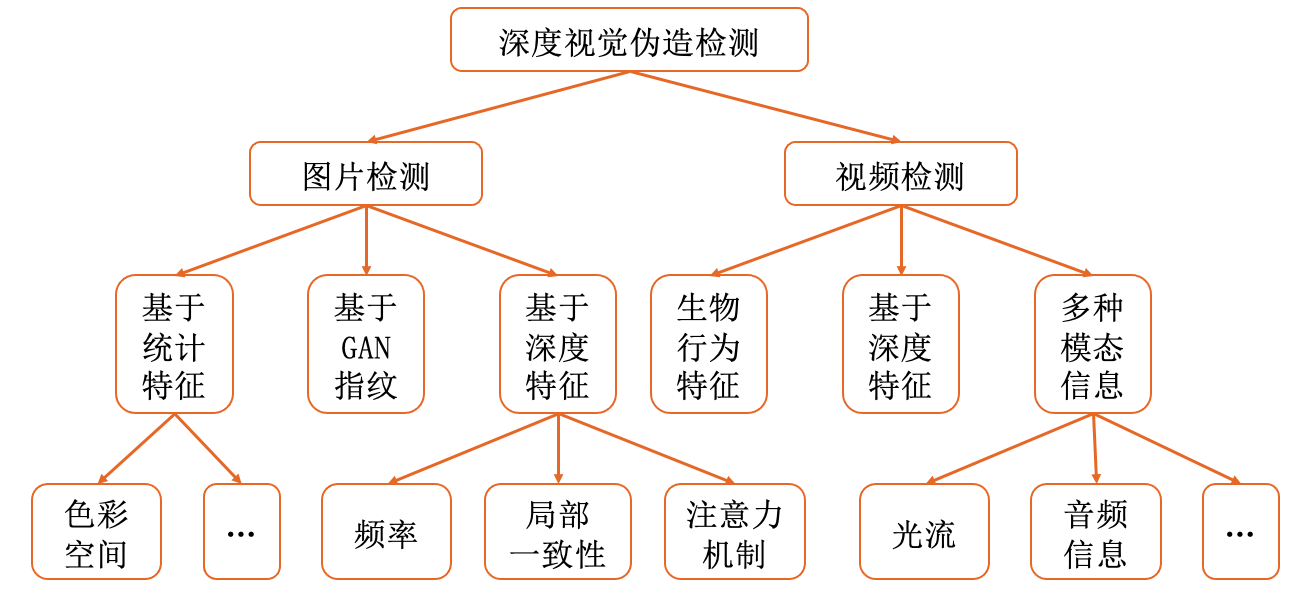
图5.4.1 深伪检测方法分类¶
5.4.2.1. 图片检测¶
基于统计特征的检测。 对深度伪造图片的检测方法通常会先将要检测的人脸提取出来,然后把提取出来的人脸图片作为检测输入,输出一个二分类结果表示人脸是真实的还是伪造的。一种被广泛应用的检测方法是基于色彩空间特征的检测,因为色彩空间特征具有很好的鲁棒性,尤其是HSV和YCbCR色彩空间,它们在伪造图像和真实图片之间往往存在很大差别。比如,Li 等人 (Li et al., 2020) 就介绍了一种基于色彩统计特征的方法;He 等人 (He et al., 2019) 进一步将其扩展到了多个色彩空间(YCbCr、HSV和Lab),然后将这些空间特征拼接起来并使用随机森林模型进行一种集成检测,获得最终的检测结果。此外,由于深度神经网络很难复制原始图像中的高频细节,因此Bai等人 (Bai et al., 2020) 提出使用频域中的统计、梯度等特征来进行深度伪造检测。
基于GAN指纹的检测。 随着生成对抗网络(GAN)的快速发展,基于GAN的深度伪造方法层出不穷,给深伪检测带来新的挑战。研究发现,GAN会在伪造图像上面留下一些“指纹”痕迹,所以可以通过寻找这些痕迹来检测由GAN伪造的图像。比如,Guarnera等人 (Guarnera et al., 2020) 使用期望最大化(expectation maximization)算法提取局部特征来对卷积痕迹进行建模,提取的特征输入到一个分类器中来完成伪造检测。但这种方法只在一个单一的尺度上捕获GAN指纹,所以检测的鲁棒性并不是很好。为了更好的解决这个问题,Ding 等人 (Ding et al., 2021) 选择采用分层贝叶斯方法(hierarchical Bayesian approach),在多个尺度上对GAN指纹进行建模,从而提高检测方法的鲁棒性。
高效检测网络设计。 也有一些工作通过设计更先进的深度特征提取网络来提高检测效果。比如,Zhou等人 (Zhou et al., 2017) 提出一种双流神经网络(two-stream neural networks):(1)使用GoogLeNet作为脸部分类流来检测人脸分类流中的篡改伪影,同时(2)使用一个基于图像块的三联体网络(triplet network)来捕捉局部噪声残余和相机特性。由于同一张图像的不同图像块之间的隐藏特征是相似的,而不同图像的图像块之间的特征是不相似的,所以用三联体网络训练出图像块的距离编码之后,利用一个SVM分类器就可以得到图像被篡改的概率。Nguyen等人 (Nguyen et al., 2019) 探索了如何使用胶囊网络(capsule networks)来检测伪造图像。Guo等人 (Guo et al., 2021) 则提出一种AMTEN(adaptive manipulation traces extraction network)预处理网络结构,其通过一个自适应卷积层来压缩图像内容,同时凸显篡改痕迹,并通过一个整合的卷积神经网络来检测虚假人脸。
篡改边界检测。 2020年,Li等人 (Li et al., 2020) 提出经典的专注于检测篡改边界的深度伪造人脸检测方法:Face X-ray。此方法首先将定位篡改区域的篡改掩码模糊处理,然后将输入图像\(x\)的Face x-ray定义为一张特殊的图像\(B\):
其中,(\(i,j\))表示像素坐标,\(M\)代表模糊边界之后的篡改掩码。如果一张人脸没有被篡改过,那么\(M\)里的值应该是全0(或者全1)。将上式计算得到的\(B\)代替原来的篡改掩码,然后和对应的人脸图片一起送入模型进行训练。具体的,给定输入图像\(x\)和其Face X-ray\(B\),模型输出伪造的概率\(\hat{c}\)和预测的Face X-ray\(\hat{B}\),训练损失函数\(\mathcal{L} = \lambda\mathcal{L}_b+ \mathcal{L}_c\)包含两个部分(\(\mathcal{L}_b\)和\(\mathcal{L}_c\)),分别定义如下:
其中,\(x\)是输入图片,\(\lambda\)用来平衡\(\mathcal{L}_b\)和\(\mathcal{L}_c\)的权重,实际训练时\(\lambda=100\),强制模型更加关注对Face X-ray的预测。上述训练可以使模型去重点学习检测篡改边界。实验表明,这种简单的训练可以获得不错的深度伪造人脸检测结果。
基于频率的检测。 深度伪造技术的快速发展使得伪造图片中的篡改痕迹越来越难以察觉,尤其是在图片经过压缩等进一步后期处理之后。不过有研究 (Durall et al., 2019, Li et al., 2004) 表明这些痕迹还可以从频域中发现,于是研究者使用频域信息作为补充,构建了更好的深度伪造检测方法。Yonghyun等人 (Jeong et al., 2022) 提出了BiHPF(bilateral high-pass filters)检测方法,通过放大合成图像中通常存在的频率伪影来完成更精确的检测。BiHPF由两个高通滤波器(HPF)组成:频率HPF用来放大高频分量中伪影的大小,同时像素HPF用来在像素域中增强人脸周围背景像素的大小。然后,利用BiHPF处理的幅度谱图作为模型的输入,训练一个基于分类的检测模型。与此前方法相比,基于频率的检测对不同篡改类型更加鲁棒。
Qian等人 (Qian et al., 2020) 提出了两种利用频率感知的伪造线索提取方法:频率感知分解(frequency-aware decomposition,FAD)和局部频率统计(local frequency statistics,LFS)。作者将这两种方法和一个交叉注意力模块相结合,组成了一个双流协作的网络**F\({^3**\)Net}来进行深度伪造检测。 在F\({^3}\)Net结构中,频率感知分解流用来发现突出的频段,而局部频率统计流用来提取本地频率统计信息。整体结构如图 图5.4.2 所示。
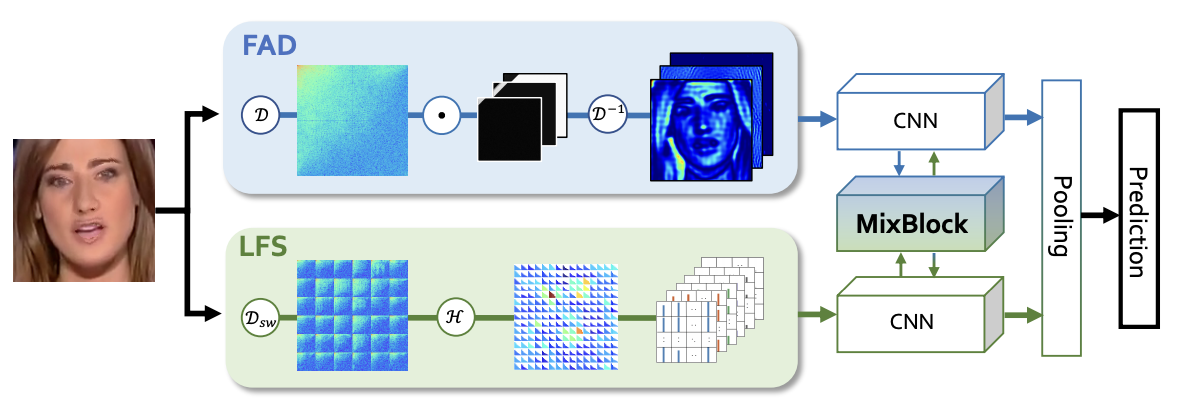
图5.4.2 F\({^3}\)Net网络结构 (Qian et al., 2020)¶
具体的,在F\({^3}\)Net中,频率感知分解流(图 图5.4.2 中的FAD模块)使用一组可学习的频率滤波器,在频域中自适应地划分输入图像,分解后的频率可以转换到空间域,从而产生一系列频率感知的图像,将这些图像在通道维度上拼接,然后输入到卷积神经网络中来提取伪造线索。 局部频率统计分解流(图 图5.4.2 中的LFS模块)首先在输入图像上使用一个滑动窗口来进行离散余弦变换(DCT),从而提取局部频率信息,然后用一组参数自适应地统计每个窗口的频率信息,再将频率统计信息重新组合成一个与输入图像大小相同的多通道空间图,之后送入卷积神经网络。最后,作者提出MixBlock结构,其使用来自两个分支的特征图来计算交叉注意力权重,以此来相互增强两个流的信息。F\({^3}\)Net使用经典的交叉熵损失函数进行训练。
基于局部一致性的检测。人脸伪造往往涉及面部区域的修改与替换,可能会造成其与周围区域在某个方面上的不一致性。为了充分利用这种局部不一致性,Zhao 等人 (Zhao et al., 2021) 提出一种“缝合”式数据合成方法不一致数据合成器(inconsistency image generator,I2G),通过变换组合不同的人脸生成大量人脸与周围区域不一致的数据,并使用此数据训练卷积神经网络分类器来完成深伪检测。实验表明,这种基于自洽性(self-consistency)的数据合成和模型训练方式可以得到较为通用的检测器。Chen等人 (Chen et al., 2021) 则是通过计算不同区域之间的相似性进行检测,也得到了不错的效果。
基于注意力机制的方法。考虑到大多数深度伪造方法只修改一小块面部区域,所以只要对这一小块面部区域给予更多关注,就可以提升检测的性能。受此启发,研究者提出了一系列基于注意力机制的检测方法。比如,Chen等人 (Chen and Yang, 2021) 先从面部分离出眼睛、嘴巴等区域,然后用注意力模型分别去检测这些区域,但这种方法需要先手动分割区域,这部分限制了它的代表能力。Zhao等人 (Zhao et al., 2021) 则组合了多个空间注意力头,可以自动使用卷积层来关注不同的局部信息。Wang等人 (Wang and Deng, 2021) 推出了一个基于注意力的数据增强框架来鼓励检测模型去关注一些细微的伪造痕迹,其通过在模型生成注意力图之后,遮挡住面部的一些敏感区域来促使检测模型去重新关注之前忽略的区域。为了学习真实的人脸与伪造的人脸之间的普遍差异(而不仅局限于某种伪造),Cao等人 (Cao et al., 2022) 提出了使用重建引导的注意力模块来增强差异特征学习,同时使用“重建-分类”学习方式来训练检测模型,其中重建学习用来提升特征学习对通用伪造模式的感知,同时分类学习用来挖掘真假人脸图像之间的本质差异。
基于对比学习的检测。图像在传播过程中经常被压缩,而现有深伪检测方法在检测被压缩的伪造图像时,存在一定的性能下降。为了对图像压缩的鲁棒性,Cao等人 (Cao et al., 2021) 将一对(原始伪造图片,压缩伪造图片)编码到压缩不敏感的嵌入特征空间,让原始和压缩伪造图片之间的距离最小,同时让真实图片和伪造图片之间的距离最大,从而形成一种对比学习方式。此方法是一种实例级(instance-level)的对比学习,仅限于学习粗粒度表征。Sun等人 (Sun et al., 2022) 则进一步提出一种双对比学习(dual contrastive learning)方式,通过实例间对比学习(inter-instance contrastive learning,Inter-ICL)来学习跟检测任务相关的判别特征;通过实例内对比学习(intra-instance contrastive learning,Intra-ICL)来充分建模和学习伪造人脸的局部特征不一致性。实验表明,这种双对比学习方式可以提升检测AUC。
5.4.2.2. 视频检测¶
对于深度伪造视频的检测,可以从视频中提取出单张人脸图片来进行检测,也可以利用视频中的时序信息(脸的动作、表情变化等)、音频信息来辅助检测。下面介绍几种针对深伪视频的检测方法。
基于行为特征的检测。虽然很多深伪方法可以合成逼真的人脸图像,却很难生成自然的表情动作,这启发了一些研究者基于生物行为特征来检测深度伪造视频 (Ciftci et al., 2020) 。“眨眼”就是一种常用的行为特征检测线索,因为眨眼是人类的一种无意识行为。Li等人 (Li et al., 2018) 研究发现,一些伪造方法训练时所使用的数据集中没有闭眼的人脸,导致伪造视频中的人不会眨眼睛。于是,他们将卷积神经网络和循环神经网络相结合,通过捕获视频中人脸的“眨眼”行为来进行检测。Jung等人 (Jung et al., 2020) 也对伪造视频中眨眼的模式进行了详细分析,提出了DeepVision检测方法,它通过检测视频中眨眼的周期、次数和持续时间来得出检测结果,并且在多种伪造视频上取得了不错的检测准确率。
除了“眨眼”之外,嘴唇的行为 (Agarwal et al., 2020, Yang et al., 2020) 和头部的运动 (Yang et al., 2019) 同样也可以帮助检测。Agarwal等人 (Agarwal et al., 2020) 提出人类在发出P、B、M等字母开头的单词时,嘴唇需要闭合,而伪造视频通常不具备这一特点。最近还有研究通过视频画面来估算人的心率,从而发现伪造视频中的心率异常 (Ciftci et al., 2020, Fernandes et al., 2019) 。Fernandes等人 (Fernandes et al., 2019) 利用神经常微分方程(neural ordinary differential equations,Neural-ODE)模型来预测心率,然后进行深度伪造检测。此外,他们还发现心跳会随时间推移而改变皮肤的反射率,而深度伪造则会打破这种连续的变化。
基于深度特征的检测。Trinh等人 (Trinh et al., 2021) 尝试使用一组原型(prototype)来表示一块特征图中特定的激活模式,然后与测试视频进一步比较,根据他们的相似性做出预测。Zheng等人 (Zheng et al., 2021) 则发现伪造视频中的相邻帧之间存在不连续性,所以他们采用一个轻量级的时序Transformer来捕获时序上的不一致性信息,进而完成检测。
基于多模态信息的检测。视频中可以用到的多模态信息主要有光流(optical flow)、自带的音频等。Amerini等人 (Amerini et al., 2019) 使用视频中帧与帧之间光流的差异来检测真伪。此外,声音与画面是否同步也是判断视频是否经过伪造的一种依据,对视频的篡改往往会破坏这些同步信息,导致视频出现假唱、不自然的面部表情和嘴唇动作等不同步信息。Trisha等人 (Mittal et al., 2020) 就是利用这些多模态信息,提出了基于视听信息的检测方法,通过建模不同模态之间的依赖关系来区分真实和篡改视频。作者使用基于孪生网络(Siamese network)的结构,分别提取视频模式和音频模式特征,并通过三元损失(triplet loss)函数来约束它们之间的一致性。
实际上,视频深伪检测可能比图片深伪检测更容易一些。一方面,视频包含大量的多模态信息,向前文介绍的时序信息、行为特征信息等,都可以用来增加检测准确率。另一方面,在检测伪造视频的过程中,不同帧的检测效果是可以累加的,随着被检测出来的伪造帧越多,整个视频是伪造的置信度也就越高,而伪造视频中难免会存在留下大量痕迹的伪造帧。整体来说,深伪检测的核心挑战在于层出不穷的伪造技术和伪造内容,对检测模型的持续更新和升级提出极高的要求。此外,随着大规模生成式模型,如DALL-E 2、Stable Diffusion 2.0、Imagen等的兴起,会导致人工智能生成数据的激增,会产生更多样化的检测场景和检测需求,亟需更通用的深伪检测技术。
5.5. 本章小结¶
本章介绍了不同类型的数据防御方法,其中包括鲁棒训练(章节 5.1节 )、差分隐私(章节 5.2节 )、联邦学习(章节 5.3节 )、篡改和深伪检测(章节 5.4节 ),分别对应上一章节中介绍的数据投毒(章节 4.1节 )、隐私攻击(章节 4.2节 )、数据窃取(章节 4.3节 )和篡改与伪造(章节 4.4节 )。鲁棒训练针对数据投毒攻击,通过提高训练算法对异常训练数据的鲁棒性来训练安全干净的模型。差分隐私通过向模型输入、模型参数、模型输出、或者目标函数中添加特定分布的噪声来获得对应预算的隐私保护性,可以防御逆向工程、隐私攻击或者数据窃取类的攻击。联邦学习则提供了一种数据隐私保护的联合训练新范式,各参与方可以在不需要公开本地数据的前提下联合训练一个强大的全局模型。当然联邦学习也面临新的数据安全问题,如隐私攻击、投毒攻击、后门攻击等,而防御这些攻击则需要一个全面鲁棒的梯度聚合算法。本章的最后还介绍了篡改与伪造数据的检测方法,包括检测通用篡改和深度伪造,这些方法通过定位并追踪伪造痕迹来检测合成数据。通过这些介绍,读者可以初步的了解当前研究在数据防御方面所作出的探索,启发未来设计更高效、更通用的数据防御技术。
