10. 模型安全：窃取攻防¶

近年来，深度学习模型由于其出色的性能，被广泛应用于计算机视觉、语音识别和自然语言处理等领域。与传统机器学习不同，深度学习模型对数据、算法和算力的要求都比较高，模型的训练往往耗资巨大，需要海量数据、先进算法和强大算力的支撑。一旦这些模型发生泄露或者被窃取则会给模型拥有者带来巨大的经济损失，严重时甚至会威胁国家安全和社会稳定。这一章将分别介绍模型窃取方面的攻击和防御方法。

10.1. 模型窃取攻击¶

模型窃取攻击的目标是通过一定手段窃取得到一个跟{受害者模型}功能和性能相近的窃取模型，从而避开昂贵的模型训练并从中获益。模型窃取是一种侵犯人工智能模型知识产权的恶意攻击行为。实际上，对人工智能模型知识产权的侵犯不仅限于模型窃取技术，未经授权的模型复制、微调、迁移学习（微小模型修改+微调）、水印去除等也属于模型知识产权侵犯行为。相比之下，模型窃取攻击更有针对性、威胁更大，即使目标模型是非公开的，很多窃取方法也能通过模型服务API完成窃取。这给模型服务提供商带来巨大的挑战，要求他们不仅要满足所有用户的服务请求还要有能力甄别恶意的窃取行为。

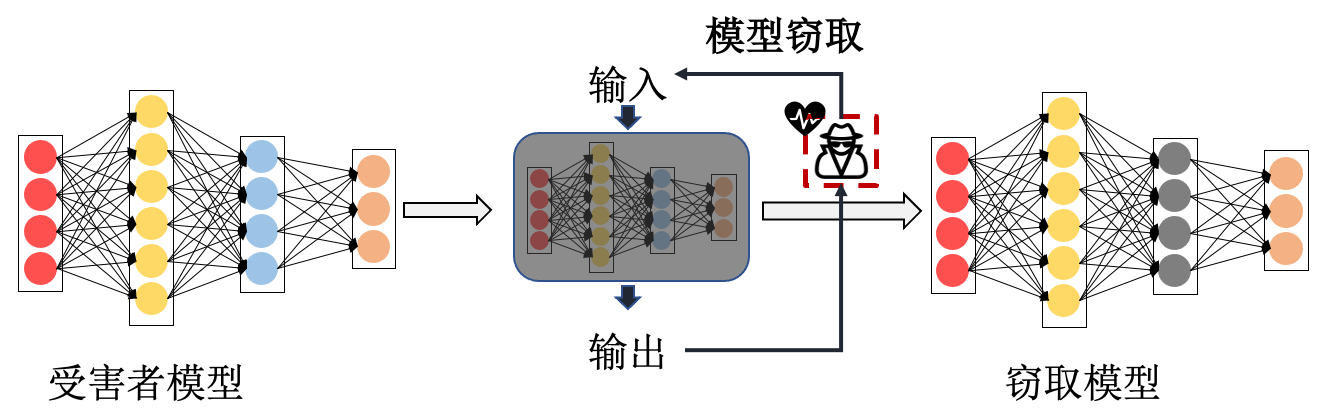
图10.1.1 模型窃取攻击示意图¶

如图10.1.1 所示，模型窃取可以在与受害者模型交互的过程中完成。攻击者通过有限次数的黑盒访问受害者模型的API接口，向模型输入不同的查询样本并观察受害者模型输出的变化，然后通过不断地调整查询样本来获取受害者模型更多的决策边界信息。在此交互过程中，攻击者可以通过模仿学习得到一个与受害者模型相似的窃取模型，或者直接窃取受害者模型的参数和超参数等信息。

一般来说，模型窃取攻击的主要目标包括：

低代价：以远低于受害者模型训练成本的代价获得一个可免费使用的窃取模型；
高收益：窃取得到的模型与受害者模型的功能和性能相当；
低风险：在窃取过程中可以避开相关检测并在窃取完成后无法被溯源。

其中，“无法被溯源”可以通过移除模型中的水印、修改模型指纹、正则化微调等后续技术改变窃取模型，使其与原始受害者模型之间产生大的差异，包括模型参数、功能、性能、属性等方面的差异。攻击者甚至可以往窃取模型中注入新的水印，以证明模型是属于自己的。

目前，大量的机器学习服务供应商将机器学习模型托管在云端服务器上，例如亚马逊AmazonML、微软AzureML、谷歌Prediction API、BigML等机器学习即服务(MLaaS)平台。MLaaS可以方便用户通过API付费使用已训练好的模型，获得特定输入的预测结果。MLaaS的接口服务模式存在一定的模型泄露风险，攻击者可以在不需要很多先验知识的前提下，通过多次查询访问接口从MLaaS中窃取模型。根据窃取方式的不同，现有模型窃取攻击可大致分为：基于方程式求解的窃取攻击、基于替代模型的窃取攻击和基于元模型的窃取攻击。

10.1.1. 基于方程式求解的窃取攻击¶

基于方程式求解的模型窃取攻击（equation-solving based attack）的主要思路是，攻击者\(A\)根据受害者模型\(f\)的相关信息构建方程式，进而基于受害者模型的输入\(x\)和输出\(f(\mathbf x)\)（如概率向量）求解方程得到与受害者模型相似的模型参数（即窃取模型\(f'\)）。图10.1.2 展示了此类攻击的一般流程。

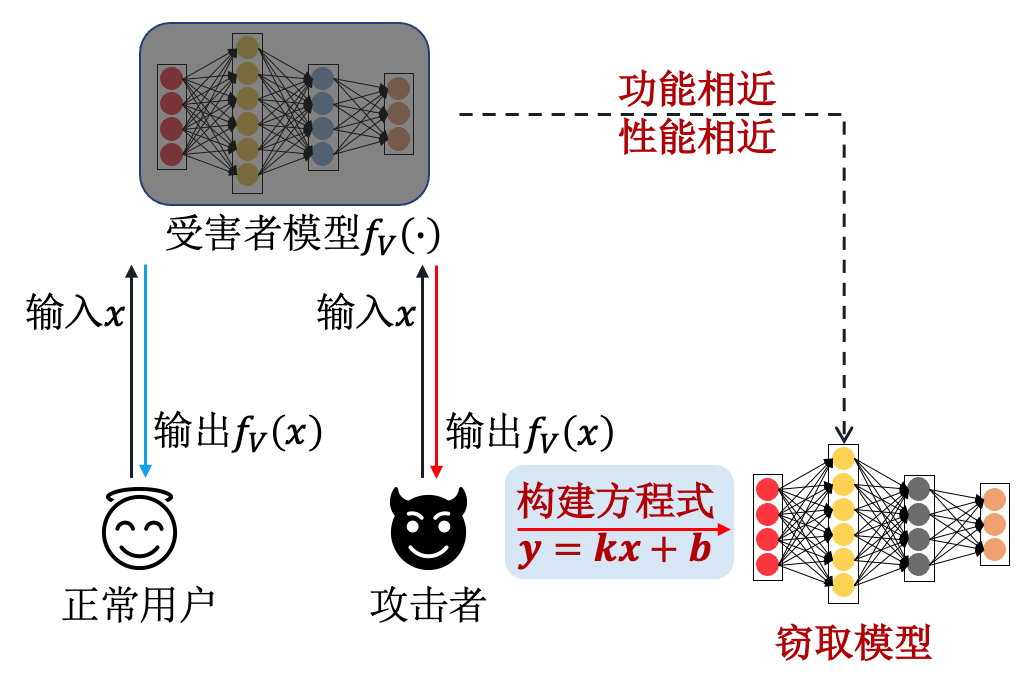
图10.1.2 基于方程式求解的模型窃取攻击流程图¶

早在2016年，Tramèr等人 (Tramèr et al., 2016) 便提出通过求解模型结构方程式来窃取机器学习模型参数。在该攻击方法中，攻击者向受害者模型发送大量查询并构建模型参数方程式，随后通过受害者模型返回的预测输出来窃取模型参数。如果受害者模型有\(d\)个参数，那么\(d+1\)个查询样本是求解模型参数\(\theta\)方程式的充分必要条件。故攻击者可以执行大于\(d+1\)次的输入查询来求解方程式，精准获得\(d\)个模型参数。以逻辑回归模型为例，其线性方程由下式给出：

(10.1.1)¶\[\begin{aligned}\theta^{\top} x=\sigma^{-1}(f( x)),\end{aligned}\]

其中，\(\theta\in\mathbb{R}^d\)为受害者模型参数，\(\sigma(t)=1/(1+e^{-t})\)为sigmoid激活函数，\(f( x)=\sigma(\theta^{\top} x)\)为受害者模型的输出。该攻击是一种针对传统机器学习模型的窃取攻击，适用于逻辑回归、多层感知机、支持向量机和决策树等机器学习模型，并不适用于复杂的深度神经网络模型。

除了模型参数，算法超参也容易被窃取，因为很多时候调参的代价要远高于训练一次模型的代价。在此前研究的基础上，Wang和Gong (Wang and Gong, 2018) 在已知训练集和模型的前提下，提出一种可以准确窃取算法超参数的方法。由于受害者模型参数通常对应的是损失函数\(\mathcal{L}(\theta)=\mathcal{L}( x,y,\theta)+\lambda R(\theta)\)的最小值，此时损失函数的梯度应为零（虽然实际情况下并非如此），则超参数\(\lambda\)的方程可由下式给出：

(10.1.2)¶\[\begin{aligned}\frac{\partial \mathcal{L}(\theta)}{\partial \theta} = b + \lambda a = 0\end{aligned}\]

(10.1.3)¶\[\begin{split}b=\begin{bmatrix}\frac{\partial \mathcal{L}( x,y,\theta)}{\partial \theta_1}\\\frac{\partial \mathcal{L}( x,y,\theta)}{\partial \theta_2}\\\dots\\\frac{\partial \mathcal{L}( x,y,\theta)}{\partial \theta_n}\\\end{bmatrix}, \; a=\begin{bmatrix}\frac{\partial R(\theta)}{\partial \theta_1}\\\frac{\partial R(\theta)}{\partial \theta_2}\\\dots\\\frac{\partial R(\theta)}{\partial \theta_n},\\\end{bmatrix}\end{split}\]

其中，训练数据集\(D=\{ x,y\}_{i=1}^{n}\)，模型参数\(\theta\)，正则项\(R\)，均为已知。故可通过最小二乘法求解超参数\(\lambda\)的方程式：

(10.1.4)¶\[\begin{aligned}\hat{\lambda}=-( a^{\top} a)^{-1} a^{\top} b.\end{aligned}\]

该攻击将超参数、模型参数和训练数据集之间的关系构建成方程式，并证明了机器学习算法的超参数同样也可以被窃取。

10.1.2. 基于替代模型的窃取攻击¶

基于替代模型的模型窃取攻击（surrogate-model based Attack）的主要思路是，攻击者\(A\)在不知道受害者模型\(f(\cdot)\)任何先验知识的情况下，向受害者模型输入查询样本\(x\)，得到受害者模型的预测输出\(f( x)\)。随后，攻击者根据输入和输出的特定关系构建替代训练数据集\(D'=\{( x,f( x))\}_{i=1}^{m}\)。值得一提的是，替代数据集\(D'\)实际上已经完成了对原始训练数据的（部分）窃取。在替代数据集\(D'\)上多次训练之后便可得到一个与受害者模型\(f(\cdot)\)功能和性质类似的替代模型\(f'(\cdot)\)，完成模型窃取攻击。图10.1.3 展示了此攻击的流程。

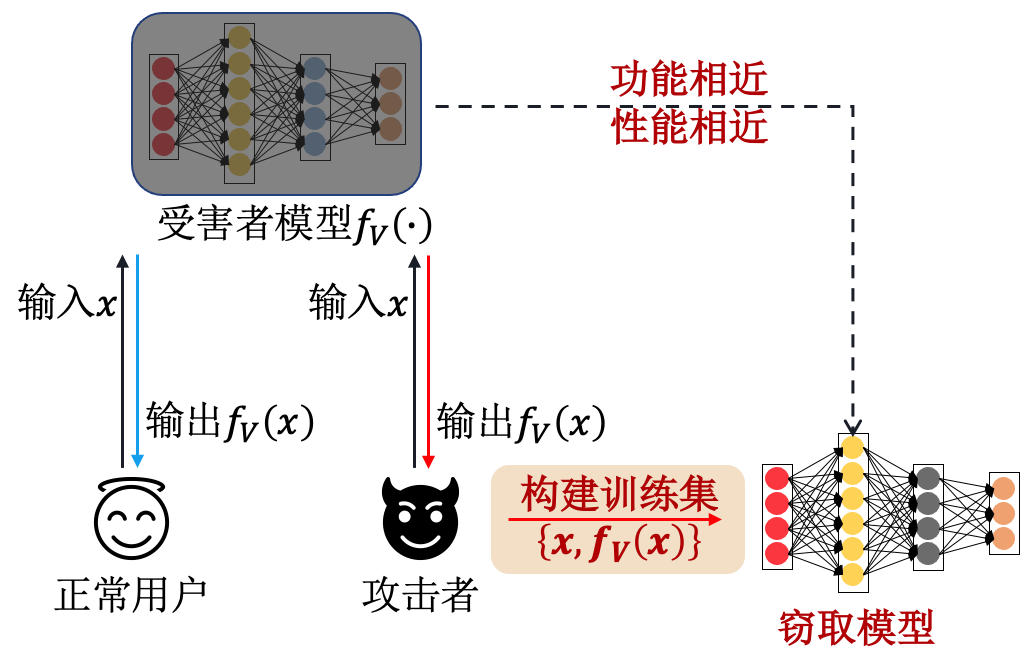
图10.1.3 基于替代模型的窃取攻击流程图¶

不难发现，模型窃取与知识蒸馏的过程相似，但也并不完全相同，这里给出二者损失函数的区别：

(10.1.5)¶\[\begin{split}\begin{aligned}\mathcal{L}_{\text{KD}} = \lambda_{1} \mathcal{L}_{\text{CE}}(y,f_{S}( x)) + \lambda_{2} \mathcal{L}_{\text{CE}}(f_{T}^{\tau}( x),f_{S}^{\tau}( x))\\\mathcal{L}_{\text{Extr}} = \mathcal{L}_{\text{CE}}(f( x),f'( x)),\end{aligned}\end{split}\]

其中，\(\mathcal{L}_{\text{KD}}\)为知识蒸馏损失，\(\mathcal{L}_{\text{Extr}}\)为模型窃取损失，\(y\)为真实标签（硬标签），\(f_{T}( x)\)和\(f_{S}( x)\)分别为教师模型和学生模型输出的预测输出（软标签），\(\tau\)为温度超参，\(f( x)\)和\(f'( x)\)分别为受害者模型和窃取模型的预测输出。可以看出，知识蒸馏的目的是将教师模型学到的特征表示蒸馏到学生模型中，而模型窃取的目的是重建一个与受害者模型一样的替代模型。

介绍到这里我们不难发现，模型窃取不仅与知识蒸馏有一定的相似性，而且使用的技术，如模型查询、替代模型等，与章节 6.2节中介绍的黑盒对抗攻击也有一定的重合。实际上，这两类攻击确实有共通之处，黑盒对抗攻击是通过查询、替代模型等技术来获取关于目标模型决策边界的知识，从而可以产生更强的攻击；而模型窃取攻击则是通过类似的探索技术来估计目标（受害者）模型的输出分布，从而获取从输入到输出的映射函数（即目标模型所代表的决策函数），以达到模型参数窃取的目的。

实际上，模型窃取和黑盒对抗攻击可以进一步结合产生更强的对抗攻击方法。比如，Papernot等人在2017年 (Papernot et al., 2017) 就提出过一种利用替代模型来增强黑盒对抗攻击的方法。此攻击先通过窃取技术得到一个近似于受害者模型决策边界的替代模型，然后基于替代模型生成对抗样本并利用对抗样本的迁移性攻击受害者模型。具体的，攻击者先收集能代表受害者模型输入域的少量数据，然后通过查询受害者模型的预测输出构建替代模型的替代训练集，此数据集比较好的刻画了受害者模型的决策边界。替代训练集可以进一步利用数据合成技术进行扩充。扩充后的数据集可以充分训练一个拟合受害者模型决策边界的替代模型。其中，迭代的数据合成过程定义如下：

(10.1.6)¶\[\begin{aligned}D'_{t+1} = \{ x + \lambda \cdot \text{sign}(J_{f'}[f( x)]): x \in D'_{t} \} \cup D'_{t},\end{aligned}\]

其中，\(\lambda\)为步长，\(f'\)为替代模型，\(J_{f'}\)为基于黑盒目标模型\(f\)的输出计算得到的雅可比矩阵，\(\text{sign}(\cdot)\)为符号函数，\(D'_{t}\)为第\(t\)次迭代时得到的数据集。公式 (10.1.6) 的目的是利用数据合成技术扩充当前的数据集\(D'_{t}\)并获得新数据集\(D'_{t+1}\)，使得新数据集能够更好的贴近受害者模型的决策边界。在替代数据集\(D'\)上训练得到替代模型后，就可以利用已有白盒攻击算法（作者使用的是FGSM (Goodfellow et al., 2015) 和JSMA (Papernot et al., 2016) ）完成黑盒迁移攻击。

Knockoff Nets攻击。一种经典的模型窃取方式是由Orekondy (Orekondy et al., 2019) 等人在2019年提出的，此攻击被命名为“仿冒网络”（Knockoff Nets）攻击。该窃取攻击无需受害者模型的先验信息，攻击者\(A\)只需构建迁移（替代）数据集\(D'(X)=\{( x_{i},f( x_{i}))\}_{i=1}^{m}\)，使替代模型无限逼近受害者模型的数据分布，进而实现模型窃取。对此攻击来说，最重要的一步是构建迁移数据集\(D'\)来向目标模型发起查询。研究者提出两种构建策略：

随机策略：攻击者从一个大规模公开数据集（如ImageNet）分布中随机抽取样本\(x \stackrel{iid}{\sim} P_{A}(X)\)；
自适应策略：攻击者利用强化学习从大规模公开数据集中选择更有利于窃取的样本\(x \sim \mathbb{P}_{\pi}(\{ x_{i},y_{i}\}^{t-1}_{i=1})\)（\(\mathbb{P}_{\pi}\)为强化学习得到的采样策略，\(x_i \sim P_A(X)\)）。

此前的大多数工作都只关注窃取模型的准确率，Jagielski等人 (Jagielski et al., 2020) 从高准确率（high accuracy）和高保真度（high fidelity）两个不同角度分析了模型窃取攻击。攻击者窃取模型的目的不同，高准确率窃取希望窃取得到的模型能对任何输入进行正确的分类，而高保真度窃取希望窃取模型与受害者模型的决策边界高度一致，二者的区别如图10.1.4 所示。

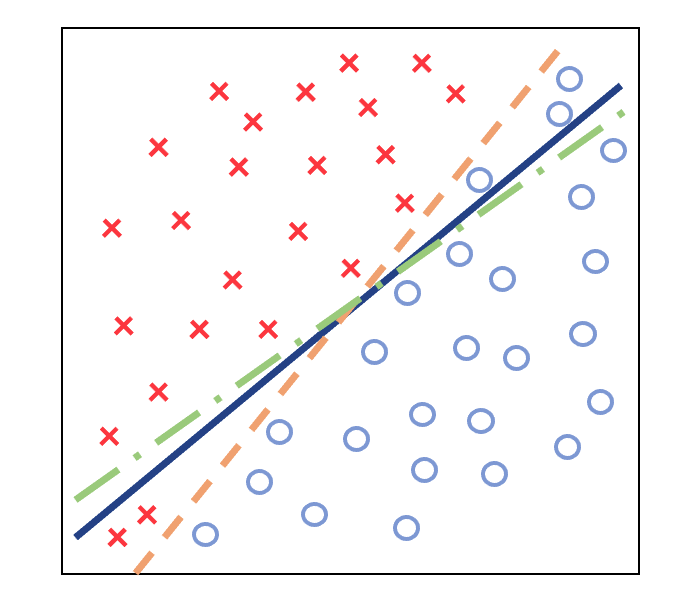
../_images/10.4_accuracy_vs_fidelity.png

图10.1.4 高准确和高保真模型窃取：蓝色、橙色和绿色线分别表示受害者、高准确窃取和高保真窃取模型的决策边界 (Jagielski et al., 2020)¶

具体来说，高准确率窃取得到的模型\(f'(\cdot)\)可以实现准确的预测，对任何输入查询\(x\)都返回正确的预测输出\(\mathop{\mathrm{arg\,max}}(f'( x)) =y\)，其目标是高度匹配甚至超过受害者模型的准确度。高保真度窃取得到的模型\(f'(\cdot)\)可以完全匹配受害者模型\(f(\cdot)\)本身，对任何输入查询\(x\)返回预测输出\(\mathop{\mathrm{arg\,max}}(f'( x)) =\mathop{\mathrm{arg\,max}}(f( x)))\)，其目的是保持与受害者模型输出的高度一致性。同时，Jagielski等人提出的高保真模型窃取方法可以在不需要梯度的情况下，通过寻找ReLU分段函数临界点窃取神经网络的权重。该方法以实验的方式完成了对两层神经网络的窃取，并从理论的角度扩展到深度神经网络。此外，高保真窃取到的模型可以作为替代模型用以其他类型的攻击，如对抗攻击和成员推理攻击。

密码分析模型提取。Carlini等人 (Carlini et al., 2020) 提出密码分析模型提取（cryptanalytic model extraction）算法，将模型窃取建模为密码分析问题进行解决，并引入差分攻击实现高保真模型窃取。该方法依赖于ReLU激活函数的二阶导数\(\frac{\partial^2 f}{\partial x^{2}} = 0\)，利用分段函数临界点来逐层窃取深度神经网络参数。具体来说，0-深度（0-deep）神经网络窃取过程如下：

(10.1.7)¶\[\begin{split}\begin{aligned}f( x) = w^{(1)} \cdot x + b^{(1)}\\f( x + e_{i})-f( x) = w^{(1)} \cdot ( x + e_{i}) - w^{(1)} \cdot x = w^{(1)} \cdot e_{i},\end{aligned}\end{split}\]

其中，\(w^{(1)}\)为参数矩阵，\(b^{(1)}\)为偏置，\(e_{i}\)为第\(i\)个神经元的标准基向量，例如\(e_{2}=[0,1,0,\ldots,0]\)。

随着神经网络层数加深，函数不再是完全线性时，则需要逐层窃取模型参数，故1层（1-deep）神经网络窃取过程如下：

(10.1.8)¶\[\begin{split}\begin{aligned}f( x) = w^{(2)} ReLU ( w^{(1)} x + b^{(1)}) + b^{(2)}\\\alpha^{i}_{+} = \frac{\partial f( x)}{\partial \epsilon e_{i}} \mid_{ x= x+ \epsilon e_{i}}\\\alpha^{i}_{-} = \frac{\partial f( x)}{\partial \epsilon e_{i}} \mid_{ x= x- \epsilon e_{i}}\\\frac{\alpha^{k}_{+} - \alpha^{k}_{-}}{\alpha^{i}_{+} - \alpha^{i}_{-}} = \frac{ w^{(1)}_{j,k}}{ w^{(1)}_{j,i}},\end{aligned}\end{split}\]

其中，\(\alpha^{i}_{+}\)和\(\alpha^{i}_{-}\)为一阶差分。假设存在\(x\)使得神经元\(j\)处于未激活状态，如果对其第\(i\)个维度上施加变化\(x+ e_{i}\)使得神经元\(j\)处于激活状态。因此\(f( x+ e_{i})-f( x)\)中存在神经元\(j\)的权重\(w^{(1)}_{j,i}\)，而\(f( x)-f( x- e_{i})\)中不存在神经元\(j\)的权重\(w^{(1)}_{j,i}\)，故可通过\(\alpha^{i}_{+} - \alpha^{i}_{-} = w^{(1)}_{j,i} \cdot w^{(2)}\)将\(w^{(1)}_{j,i}\)分离出来。随后对每个神经元重复这个过程，即可计算获得神经元权重的比例\(\frac{\alpha^{k}_{+} - \alpha^{k}_{-}}{\alpha^{i}_{+} - \alpha^{i}_{-}}\)。一旦窃取了第一层的参数，便可剥离第一层的权重矩阵和偏置，继续使用0层神经网络窃取方法窃取第二层的权重。该方法可以继续扩展到窃取k层神经网络，同样通过寻找临界点逐层窃取参数，将\(k\)层神经网络减少至\(k-1\)层神经网络，以此类推。

估计合成攻击。现有的大多数模型窃取攻击都假设攻击者拥有受害者模型训练集的全部或部分先验知识，而实际上这些私有训练集并不容易获得。因此，Yuan等人 (Yuan et al., 2022) 在2022年提出一种无需受害者模型及训练数据信息的估计合成攻击（estimation synthesis attack，ES）。该方法首先随机初始化生成一个与受害者训练集\(D\)交集很少的合成数据集\(D^{(0)}_{\text{syn}}\)，并根据合成数据集\(D^{(0)}_{\text{syn}}\)和受害者模型返回输出\(f( x)\)训练一个替代模型\(f'\)。然后迭代合成数据集和替代模型，提高合成数据的质量和替代模型的性能。

具体的，ES攻击有两个关键步骤，即E-step和S-step。首先，E-step在合成数据集上使用知识蒸馏将受害者模型\(f\)的知识蒸馏到替代模型\(f'\)中，可形式化为：

(10.1.9)¶\[\begin{split}\begin{aligned}f^{(t)}_{A} = \mathop{\mathrm{arg\,min}}\limits_{f'} \mathcal{L}_{\text{KD}}(f',f;D^{(t-1)}_{\text{syn}})\\\mathcal{L}_{\text{KD}}(f',f;D^{(t-1)}_{\text{syn}}) = \frac{1}{\left| D_{\text{syn}} \right|} \sum\limits_{ x \in{D_{\text{syn}}}} \mathcal{L}_{\text{CE}}(f( x),f'( x)),\end{aligned}\end{split}\]

其中，\(f^{(t)}_{A}\)为第\(t\)步迭代得到的替代模型，\(D^{(t-1)}_{\text{syn}}\)为前一次迭代（\(t-1\)）得到的合成数据集，\(\mathcal{L}_{\text{KD}}\)为知识蒸馏损失函数，\(\mathcal{L}_{\text{CE}}\)为交叉熵损失函数。接下来，S-step提供两种合成数据集的方法DNN-SYN和OPT-SYN。

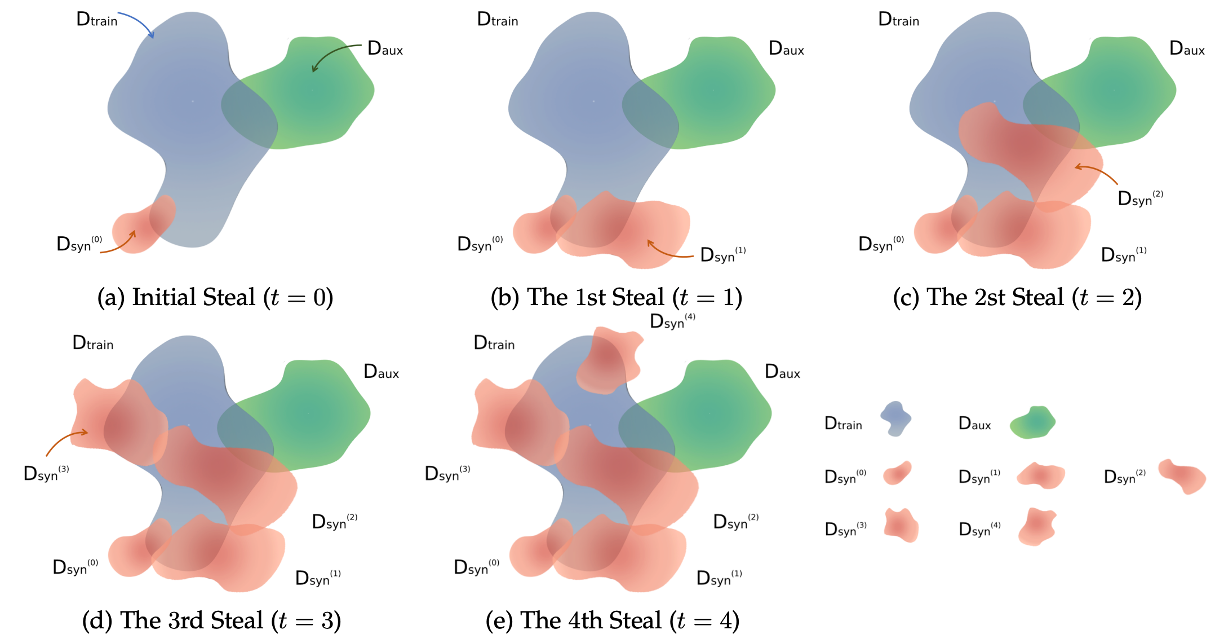
图10.1.5 ES攻击中的数据合成过程 (Jagielski et al., 2020) ：\(D_{\text{train}}\)为原始训练数据，\(D_{\text{syn}}\)为攻击合成数据，\(D_{\text{aux}}\)为额外数据（比如公共数据集）¶

DNN-SYN采用ACGAN（auxiliary classifier GAN）来生成合成数据集\(D_{\text{syn}}\)。首先，向ACGAN的生成器\(G\)中随机输入标签\(l_i\)和随机向量\(z_i\)，然后训练生成器\(G\)使得生成的数据\(D_{\text{syn}}=\{G( z_i,l_i)\}_{i=1}^{m}\)可以被替代模型\(f'\)分类为标签\(l_i\)，优化过程如下：

(10.1.10)¶\[\begin{split}\begin{aligned}\mathcal{L}_{\text{DNN}} = \mathcal{L}_{\text{img}} + \lambda \mathcal{L}_{\text{ms}}\\\min\limits_{ w_{G}} \mathcal{L}_{\text{img}}(G,l) = \sum^{m}_{i=1} \mathcal{L}_{\text{CE}}(f'(G( z_i,l_i)),l_i)\\\mathcal{L}_{\text{ms}}(G,l) = \sum^{m}_{i=1} \frac{d( z^1_i, z^1_2)}{d(G( z^1_i,l_i),G( z^2_i,l_i))},\end{aligned}\end{split}\]

其中，\(\mathcal{L}_{\text{img}}(G,l)\)为合成数据集的损失函数，\(\mathcal{L}_{\text{ms}}(G,l)\)为防止生成模型崩溃的模式搜索（mode seeking）正则化项，\(d(\cdot)\)为距离度量。

为了避免模型崩塌（mode collapse），S-step还可以采用OPT-SYN方法合成数据集，思想是让替代模型\(f'\)对合成数据\(x'\)的预测结果\(f'( x')\)与随机采样的标签\(y\)尽可能的接近。OPT-SYN方法的优化过程如下：

(10.1.11)¶\[\begin{aligned}x' \gets \mathop{\mathrm{arg\,min}}\limits_{ x} \mathcal{L}_{\text{CE}}(f^{(t)}_{A}( x),y),\end{aligned}\]

其中，\(f^{(t)}_{A}\)为第\(t\)步迭代得到的替代模型，\(x'\)是新的合成样本，\(y\)是从狄利克雷分布（Dirichlet distribution）中采样而来的预测标签。最终，ES攻击反复迭代E-step和S-step，使合成数据集逼近受害者的私有训练数据集，同时替代模型无限逼近受害者模型。图图10.1.5 展示了ES攻击中的数据合成过程，其中合成方法可以是DNN-SYN也可以是OPT-SYN。

10.1.3. 基于元模型的窃取攻击¶

基于元模型的模型窃取攻击（meta-model attack）的主要思路是，攻击者\(A\)通过训练一个元模型\(\Phi(\cdot)\)，将受害者模型的预测输出\(f( x)\)作为元模型的输入，将受害者模型的参数信息作为元模型的输出\(\Phi(f( x))\)。因此，该方法需要攻击者\(A\)准备大量与受害者模型功能相似的模型\(f \sim \mathcal{F}\)来构建元模型的训练数据集\(\{f( x),\Phi(f( x))\}\)。经过多次训练之后，该元模型\(\Phi(\cdot)\)就可以窃取受害者模型\(f(\cdot)\)的属性信息，即激活函数、网络层数、优化算法等信息。其流程如图10.1.6 所示。

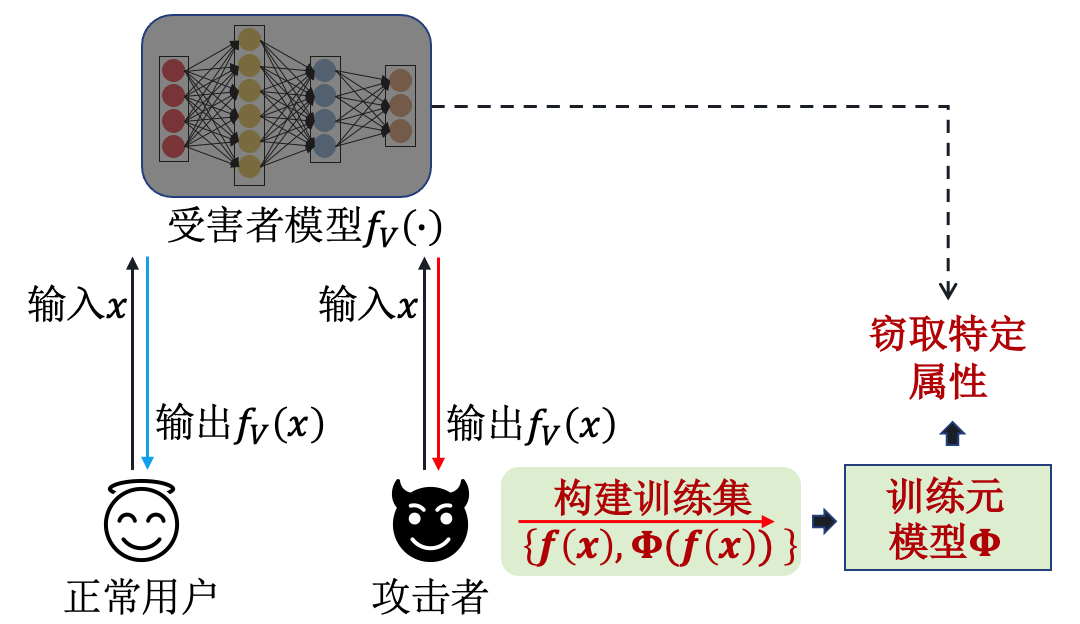
图10.1.6 基于元模型的窃取攻击流程图¶

元模型窃取攻击由Oh等人 (Oh et al., 2019) 在2019年提出，并在MNIST数据集上成功窃取了受害者模型的属性信息（model attributes），包括模型架构、优化器和数据信息。给定想要窃取的模型属性\(a\)，如激活函数、卷积核大小、批大小、数据大小等12个属性，元模型窃取攻击通过求解下面的优化问题来训练元模型：

(10.1.12)¶\[\begin{aligned}\min\limits_{\theta} \mathop{\mathbb{E}}\limits_{f \sim \mathcal{F}} \left[\sum^{12}_{a=1} \mathcal{L}_{\text{CE}} (\Phi^{a}_{\theta}([f( x_i)]^{n}_{i=1}), y^{a})\right],\end{aligned}\]

其中，\(\theta\)为元模型参数，\(\mathcal{F}\)为元训练中模型的分布，\(a\)为目标模型属性，\(y^{a}\)为模型属性的真实标签。上述损失函数\(\mathcal{L}_{\text{CE}}\)定义了输出受害者模型的属性信息\(\Phi^{a}_{\theta}([f( x_{i})]^{n}_{i=1})\)与受害者模型的真实属性信息\(y^{a}\)的距离。可以看出，构建元模型的训练数据集\(\{f( x),\Phi(f( x))\}\)需要大量任务相关的数据和模型，所以在实用性方面存在一定的局限性。

10.2. 模型窃取防御¶

模型窃取防御的目的是让攻击者无法通过简单的查询就能窃取模型参数。一般来说，模型参数的泄露是因为参数过于精确，对每一个不同的输入样本都呈现出特定的激活状态。所以可以使用模糊化技术进行防御，模糊模型参数、模糊决策边界、模糊输入概率等等，都会对窃取攻击起到一定的防御作用。当然，一定程度的“性能-安全性权衡”也是在所难免的。另外一种简单有效的防御方式是查询控制，通过直接限制用户的查询方式、查询次数等恶意查询行为来阻止模型窃取的发生。此外，在窃取发生以后，我们也需要模型溯源技术，对窃取模型进行溯源追踪、调查取证，从而可以通过法律手段来保护模型所有者的权益。下面我们将简要介绍这三类模型窃取防御技术。

10.2.1. 信息模糊¶

信息模糊防御旨在保证模型性能的前提下，对模型的输出进行模糊化处理，尽可能的扰动输出向量中的敏感信息，从而保护模型隐私。由于攻击者所需的输入正好是受害者模型返回的输出，因此窃取防御需要在不影响受害者模型性能的前提下，模糊处理攻击者可获得的敏感信息，从而实现信息模糊防御。然而此类防御也存在一定的局限性，需要在模糊强度和性能保持方面做一个权衡，模糊化更多信息会导致模型性能下降更多，但是防御窃取攻击更有效，反之亦然。根据具体防御方法的不同，信息模糊防御又可以分为截断混淆和差分隐私。

10.2.1.1. 截断混淆¶

截断混淆的主要思想是，通过对受害者模型的输出概率向量进行模糊化操作，使得输出的向量包含更少、更粗糙的信息，从而实现窃取防御。最容易想到的模糊技术就是取整操作（rounding operation），当然如果只返回概率最大的类别也可以大幅减少攻击者可获得的信息。

于是，Fredrikson等人 (Fredrikson et al., 2015) 在2015年讨论了针对模型逆向攻击的有效防御对策，即降低攻击者从受害者模型中获取到的置信度分数的精度。该方法通过对softmax层输出的置信度分数进行四舍五入，达到对输出向量模糊的效果。实验表明，该方法可以在保持模型性能的情况下，具有抵抗窃取攻击的能力。

Shokri等人 (Shokri et al., 2017) 于2017年讨论了四种模型防御的有效对策: （1）将输出向量限制为前\(\boldsymbol{k}\)个类。该方法只输出可能性最大的\(k\)个类别，随着\(k\)值减小，模型泄漏的信息也越来越少。在极端情况下，模型只返回最大可能的类别标签; （2）将输出向量四舍五入。该方法将输出向量中的标签概率保留\(d\)位小数，随着\(d\)值减小，模型泄漏的信息越少; （3）增加输出向量的信息熵。该方法向softmax层增加温度调节参数\(\tau\)，使得\(\mathrm{softmax}\)层的输出变为\(\frac{e^{ z_{i}/\tau}}{\sum\limits_{j}e^{ z_{j}/\tau}}\)。随着\(t\)值的增大，输出向量的熵也会增大，即输出向量变得越均匀，模型泄漏的信息就越少; （4）正则化。模型越是过拟合到训练数据，就越会学到敏感的决策边界，这样会泄露更多信息，导致决策边界容易被逆向。因而，可通过向损失函数中添加\(\lambda \sum \theta^2\)正则项的方式来惩罚模型参数，避免过拟合问题的同时减少模型泄露的信息。随着\(\lambda\)的增加，模型的性能和安全性都会有所提高，但如果\(\lambda\)增加过度，则会对模型的正常训练产生负面影响，导致准确率的下降。

10.2.1.2. 差分隐私¶

差分隐私由Cynthia等人 (Dwork et al., 2006) 在2006年首次提出（详细介绍参考章节 5.2节）。随后大量研究者将机器学习与差分隐私技术结合起来用于保护模型的隐私，目标是在保证模型准确性的同时最大限度的保证模型隐私性。差分隐私 (Dwork et al., 2014) 通过添加噪声，使得差别只有一条记录的相邻数据集经过模型推理获得相同结果的概率非常接近，即抹除单个样本在模型中的区分度，从而保护模型隐私。

差分隐私在窃取防御中，可通过对模型添加随机噪声扰动，使得攻击者无法判断训练数据集的变化对模型输出的影响，有效增加攻击的难度。根据添加噪声的不同位置，基于差分隐私的防御方法可进一步分为：输出扰动、目标函数扰动和梯度扰动。

输出扰动。 Chaudhuri等人 (Chaudhuri and Monteleoni, 2008) 提出一种基于敏感度的机器学习隐私保护算法。该方法将噪声添加到逻辑回归的输出中，通过敏感度衡量模型防御能力。其中，敏感度的定义如下：

(10.2.1)¶\[\begin{aligned}S(f) = \max\limits_{ a, a'} \left| f( x_1,\ldots, x_{n-1}, x_{n} = a) - f( x_1,\ldots, x_{n-1}, x_{n} = a') \right|,\end{aligned}\]

其中，\(a\)为特征向量，\(S(f)\)为敏感度。上式敏感度的定义可理解为，当且仅当输入数据中任意一条数据改变时，其输出结果变化的最大值。

在已有研究的基础上，Zhang等人 (Zhang et al., 2017) 提出在强凸函数（strongly convex function）的情况下，通过选择合适的学习率，可以有效提高添加了输出扰动的梯度下降的效率。Wang等人 (Wang et al., 2017) 进一步讨论了输出扰动和目标函数扰动，并提出输出扰动方法在凸函数（convex function）情况下更为有效，但可能无法推广到非平滑条件下。

目标函数扰动。 Chaudhuri等人 (Chaudhuri and Monteleoni, 2008) 还提出一种目标函数扰动方法，用正则化常量\(\mathit{\lambda}\)替代原本添加噪声进行输出扰动的方法。正则化是一种防止模型过拟合到训练数据的常用技术，但是在该方法中，正则化用来降低模型对输入变化的敏感度，从而达到保护模型隐私的目的。目标函数扰动方法的形式化定义如下：

(10.2.2)¶\[\begin{aligned}y' = \mathop{\mathrm{arg\,min}}\limits_{\theta} \frac{1}{2} \lambda \theta^{\top} \theta + \frac{ b^{\top} \theta}{n} + \frac{1}{n} \sum^{n}_{i=1} \log(1+e^{-y_{i} \theta^{\top} x_{i}}),\end{aligned}\]

其中，\(b\)为随机向量，\(\lambda\)为正则化常数。此外，Chaudhuri等人还揭示了正则化和隐私保护之间的关系，即正则化常数越大，逻辑回归函数的敏感度就越低，因此为保持其隐私需要添加的噪声也就越少。也就是说，正规化不仅可以防止过度拟合，还有助于保护隐私。

梯度扰动。 Song等人 (Song et al., 2013) 提出差分隐私随机梯度下降（differentially private SGD， DP-SGD）和差分隐私批量随机梯度下降（differentially private Mini-batch SGD）方法来保护数据隐私（同样适用于保护模型隐私）。该方法在原来梯度的基础上添加噪声来实现差分隐私，适用于凸目标函数。基于单点（single-point）数据的DP-SGD通过以下方式更新模型参数：

(10.2.3)¶\[\begin{aligned}\theta_{t+1} = \theta_{t} - \eta_{t}(\lambda \theta_{t} + \nabla \mathcal{L}(\theta_{t},x_t,y_t) + Z_t),\end{aligned}\]

其中，\(\theta\)为模型参数，\(\eta\)为步长，\(Z_t \in \mathbb{R}^d\)为从密度分布\(\rho( z)=e^{\frac{\alpha}{2}\|z\|}\)中独立采样的\(d\)维随机噪声向量。在单点DP-SGD的基础上增加批量大小，Song等人进一步提出了下述批量DP-SGD算法：

(10.2.4)¶\[\begin{aligned}\theta_{t+1} = \theta_{t} - \eta_{t}(\lambda \theta_{t} + \frac{1}{b} \sum\limits_{( x_i,y_i) \in B_t} \mathcal{L}(\theta_{t}, x_i,y_i) + \frac{1}{b} Z_t)，\end{aligned}\]

其中，\(b\)为批量大小，\(\mathcal{L}\)为分类损失函数如交叉熵。实验表明，适度增加批量可以显着提高性能。

Abadi等人 (Abadi et al., 2016) 将深度学习与差分隐私相结合，提出了一个改进版的DP-SGD算法来处理非凸目标函数。该方法在梯度中添加噪声，在合适的隐私预算内训练神经网络。差分隐私随机梯度下降计算过程如下：

(10.2.5)¶\[\begin{split}\begin{aligned}g_t( x_i) \gets \nabla_{\theta_{t}} \mathcal{L}(\theta_y, x_i)\\\bar{g}_t( x_i) = g_t( x_i) / \max(1,\frac{{\Vert g_t( x_i) \Vert}^2}{C})\\\tilde{g}_t( x_i) = \frac{1}{L} (\sum\limits_i \bar{g}_t( x_i) + \mathcal{N}(0,\sigma^2 C^2))\\\theta_{t+1} = \theta_{t} + \eta_t{g}_t( x_i),\end{aligned}\end{split}\]

其中，\(x\)为输入样本，\(\theta\)为模型参数，\(\mathcal{L}(\theta)=\sum_{i}\mathcal{L}(\theta, x_{i})\)为损失函数，\(\bar{g}_t( x_i)\)为范数裁剪（norm clipping）后的梯度，\(C\)为梯度范数边界，\(\tilde{g}_t( x_i)\)为加入噪声的梯度，\(\sigma\)为参数噪声。公式 (10.2.5) 的目的是利用差分隐私向梯度中增加噪声实现梯度扰动，随后计算全局的隐私预算，在一定的隐私预算下保护模型隐私。

10.2.2. 查询控制¶

查询控制防御在保证用户正常使用模型API接口的情况下，根据用户查询行为进行判别，分辨出正常用户和攻击者，从而在模型输入阶段实现精准控制与防御。直观来讲，模型窃取者需要不断的变换输入样本来刺探模型的参数和决策边界，需要多样的输入来覆盖更大的测试空间，就好像是在尝试完成一个“拼图”。这种行为与普通的API接口使用有很大的区别，可以利用这种区别来检测模型窃取行为，即所有尝试完成“拼图”的查询行为都有可能是窃取。

不难想到，一种最简单的防御策略就是控制所有用户的查询次数和查询频率，一方面可以降低被且窃取的风险，另一方面可以降低服务器的计算压力，一举两得。实际上，很多国际互联网公司就是通过这种策略来控制免费用户的查询权限的。当然，这会带来很不好的用户体验，尤其是针对付费用户时。更灵活一点，那就是按照查询行为进行检测，根据每个用户自己的行为特点进行查询控制。

一般来说，窃取模型需要对目标模型发起大量访问，并且窃取查询样本应该与正常查询样本具有不同的分布。基于此假设，Juuti等人 (Juuti et al., 2019) 在2019年首次提出一种检测模型窃取攻击的方法PRADA（protecting against DNN model stealing attacks）。该方法假设正常用户的查询样本之间的距离接近正态分布（即自然样本符合自然分布），而攻击者合成的查询样本之间的距离会严重偏离正态分布（即人造样本偏离自然分布）。

具体来说，PRADA方法计算一个查询样本\(x_i\)与其同类别\(f( x_i)=y\)的先前查询样本\(\{x_0,\ldots , x_{i-1} \}\)之间的最小距离\(d_{\text{min}}( x_i)\)，并存储在集合\(D\)中。如果最小距离\(d_{\text{min}}( x_i)\)超过既定阈值\(T_c\)，则将其加入增长集合\(D_{G_{c}}\)并更新阈值\(T_c \gets \max (T_c, \bar{D_{G_{c}}} - \text{std}(D_{G_{c}}))\)，其中\(\bar{D_{G_{c}}}\)和\(\text{std}(D_{G_{c}}))\)分别为均值和方差。因此，PRADA方法不依赖于单个查询样本，而是分析多个连续查询样本的分布，并在分布偏离正常用户查询样本行为时发出警报。这种基于分布的检测可以防止因单点异常而误报警。

上述方法是基于输入分布的检测，而对深度学习模型而言，样本的特征分布比输入分布可能更有区分度。因此，Kesarwani等人 (Kesarwani et al., 2018) 提出了一种基于特征分布的模型窃取监视器，保护基于云的MLaaS服务。该方法监控用户的查询样本，通过分析查询样本的特征分布来判断模型被窃取的风险。类似的，Yu等人 (Yu et al., 2020) 提出一个单独的特征分析模型DefenseNet，来检测异常查询样本的特征分布，将神经网络的每个隐藏层的特征输出作为输入，并使用支持向量机来区分正常和攻击查询样本。

总体来说，针对模型窃取的检测和查询控制工作并没有很多。实际上，此类防御方法具有广阔的应用前景，尤其是未来MLaaS会服务于千百万用户，每天都会面临各种各样的风险，需要随时检测并防御恶意用户的攻击。在这种情况下，窃取检测需要对用户的查询行为进行更全面的刻画，建立用户画像，同时要结合模型本身的参数、决策边界、泛化特点等，建立对要保护模型更有针对性的检测方法，并通过灵活的调整对不同用户的查询控制来达到既能保护模型隐私又不影响服务质量的防御体系。

10.2.3. 模型溯源¶

当模型泄露已经发生时，模型所有者需要通过溯源技术证明窃取者所拥有的模型来自于防御者，即两个模型是同源的且窃取模型是受害者模型的衍生品，以此帮助模型拥有者在知识产权诉讼过程中掌握主动权。目前领域内还没有工作能同时达到这两个目标。现有模型溯源方面的方法大致可以分为两类：模型水印和模型指纹。二者工作原理不同，对应的优缺点也不同。下面详细介绍这两类方法。

10.2.3.1. 模型水印¶

向模型中添加所有者印记（如公司logo）是一种最直接的模型版权保护方法，这样就可以通过验证所有者印记来对模型进行溯源。基于此想法，研究者提出模型水印（model watermarking）的概念，将数字水印（digital watermarking）的概念从多媒体数据版权保护推广到深度神经网络模型知识产权保护。但是，人工智能模型与多媒体数据有很大差异，需要特殊的水印嵌入和提取方式 (谢宸琪 et al., 2021) 。

一般的，模型水印可分为水印嵌入（watermark embedding）和水印提取（watermark extraction）两个步骤。如何设计高效、鲁棒的模型水印嵌入和提取方法是模型水印防御的关键。在水印嵌入阶段，模型所有者可以向需要保护的模型参数\(\theta\)中嵌入水印信息\(wm\)，形式化表示如下：

(10.2.6)¶\[\begin{aligned}\theta_{\text{pro}} = \lambda \cdot \theta + (1-\lambda) \cdot (\mathop{\mathrm{arg\,min}}\limits_{\theta} \mathcal{L}_{\text{wm}}(f_{\theta_{\text{pro}} }(\theta), \text{wm})),\end{aligned}\]

其中，\(\theta_{\text{pro}}\)为嵌入水印后（即受保护）的模型参数，\(\mathcal{L}_{\text{wm}}\)是引导水印嵌入的损失函数，\(f_{\theta_{\text{pro}}}(\cdot)\)是水印嵌入矩阵的函数。在水印提取阶段，模型所有者可以通过提取可疑模型中的水印\(\text{wm}'\)来验证模型的所有权，形式化表示如下：

(10.2.7)¶\[\begin{aligned}\text{Verify} = \frac{1}{N}\Sigma _{i=1}^{N}\delta(\text{wm}_i,\text{wm}'_i),\end{aligned}\]

其中，\(\delta(\cdot,\cdot)\)是一个相似度函数，衡量提取水印和原始水印的相似程度，二者越相似验证结果的置信度就越高；\(\text{wm}_i\)为第\(i\)个水印，一个模型可以嵌入多个水印。

目前，基于模型水印的人工智能模型版权保护方法可以根据适用的场景分为白盒水印和黑盒水印两大类。

（1）白盒水印

白盒水印场景假设模型所有者可以得到可疑模型的参数。在这种场景下嵌入水印时，模型所有者可以将一串水印字符串以正则化的方式直接嵌入到模型内部。在水印提取过程中，模型所有者可以直接基于可疑模型的参数尝试提取水印字符串。一旦提取成功，模型所有者便可计算真实水印\(\text{wm}\in\{0,1\}^N\)与提取水印\(\text{wm}'\in\{0,1\}^N\)之间的误码率（bit error rate, BER）来验证模型版权。其流程如图图10.2.1 所示。

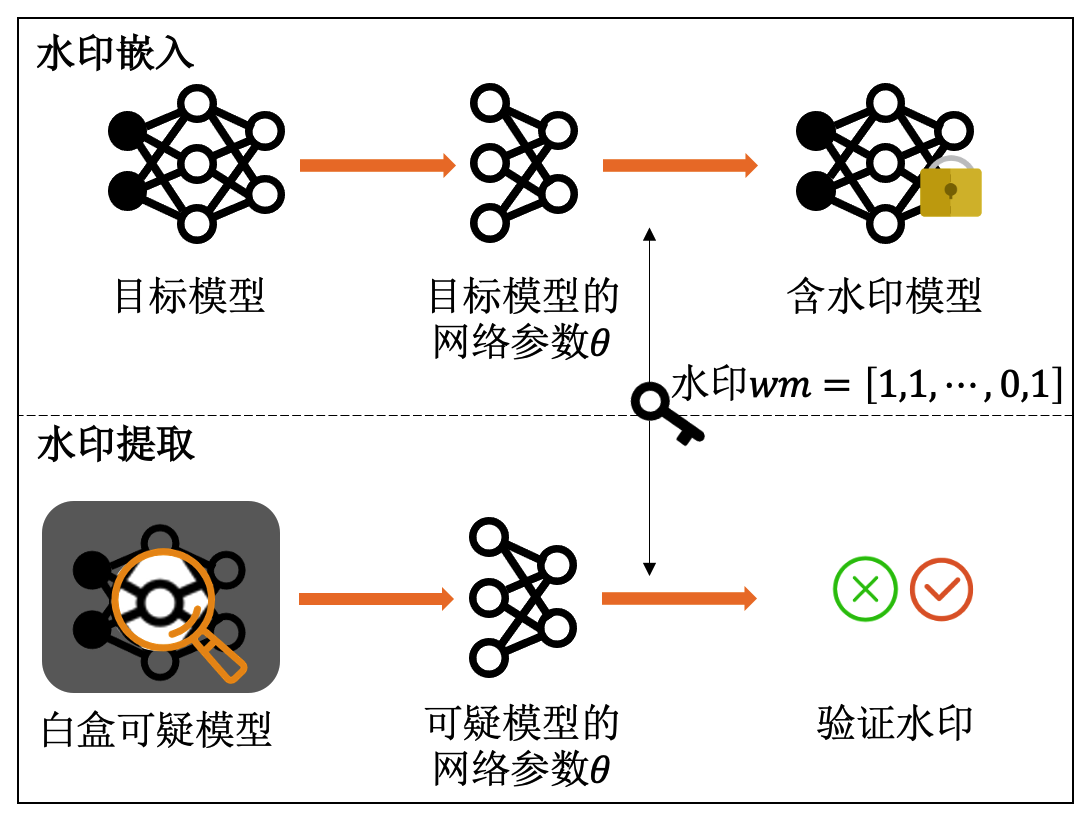
图10.2.1 白盒水印方法¶

模型水印由Uchida等人 (Uchida et al., 2017) 在2017年首次提出，其提出了一个在训练过程中向模型参数矩阵中嵌入水印的模型溯源方法。具体而言，模型所有者首先计算模型权重的均值\(\theta\)并给定嵌入矩阵\(X\)，然后通过嵌入正则化算法将\(T\)比特的水印信息\(b \in \{0,1\}^T\)嵌入到模型的参数矩阵中，这种白盒水印嵌入的目标函数是：

(10.2.8)¶\[\begin{split}\begin{aligned}\mathcal{L} = \mathcal{L}_{0}(f( x),y) + \lambda \mathcal{R}(\theta, b)\\\mathcal{R}(\theta, b) = -\sum^{T}_{j=1} ( b_j \log( z_j) + (1- b_j) \log(1- z_j) )\\ z_j=\sigma(\sum_{i} X_{ji} \cdot \theta_{i}),\end{aligned}\end{split}\]

其中，\(\mathcal{L}_{0}\)是原始任务损失函数；\(\mathcal{R}\)是对参数\(\theta\)嵌入水印的正则化项；\(X\)是嵌入矩阵，为固定参数；\(\theta\)是嵌入目标，为可学习参数；\(\sigma(\cdot)\)为sigmoid函数。需要注意的是，式 (10.2.8) 中除了\(\mathcal{L}_{0}\)项包含模型的输出\(f( x)\)，其他项都是直接在模型参数上定义的，并不涉及输入在模型中的前传操作。上式的目的是，在保证模型性能不受影响的前提下（由\(\mathcal{L}_{0}\)来保证），通过正则化将水印\(b_j\)嵌入到嵌入矩阵\(X\)（嵌入为1不嵌入为0）指定的模型参数位置中。

在水印验证的过程中，需要对可疑模型进行白盒访问，从可疑模型的参数矩阵中提取\(T\)比特的水印信息\(b'\)，提取位置依然是嵌入矩阵\(X\)定义的位置。提取过程可形式化表示为：

(10.2.9)¶\[\begin{split}\begin{aligned} b'_{j} = s(\sum_{i} X_{ji} \cdot \theta_{i})\\s(x) = \left\{\begin{array}{rcl}1\qquad x\geq0\\0\qquad \text{else},\\\end{array} \right.\end{aligned}\end{split}\]

其中，\(s(\cdot)\)是单位阶跃函数（unit step function）。最后，通过比对水印便可验证模型版权。

与此前将水印嵌入到模型的静态权重不同，Darvish等人 (Darvish Rouhani et al., 2019) 提出一种端到端的模型保护框架深度符号（DeepSigns），可将水印嵌入到模型激活层的概率密度函数（probability density function, PDF）的动态统计信息中。因为要操作中间层激活，所以此方法也是一种白盒水印方法。此外，该方法也支持向模型的输出层中嵌入水印，以便进行黑盒水印验证。

（2）黑盒水印

在黑盒水印的场景下，模型所有者（即验证者）不可访问可疑模型的内部参数，但是可以通过查询模型并观察其输出进行版权验证。黑盒水印方法通常遵循后门攻击的思路，通过让模型学习特定输入输出关联的方式达到水印嵌入和提取的目的。具体的，在水印嵌入过程中，模型所有者通过构造特定输入输出的触发（水印）数据集，在训练的过程中将触发数据学习到模型中。在水印提取时，模型所有者只需向可疑模型查询触发数据并获得模型的输，来计算模型在触发数据上的准确率（Trigger Set Accuracy, TSA），进而验证模型版权。大体流程如图图10.2.2 所示。

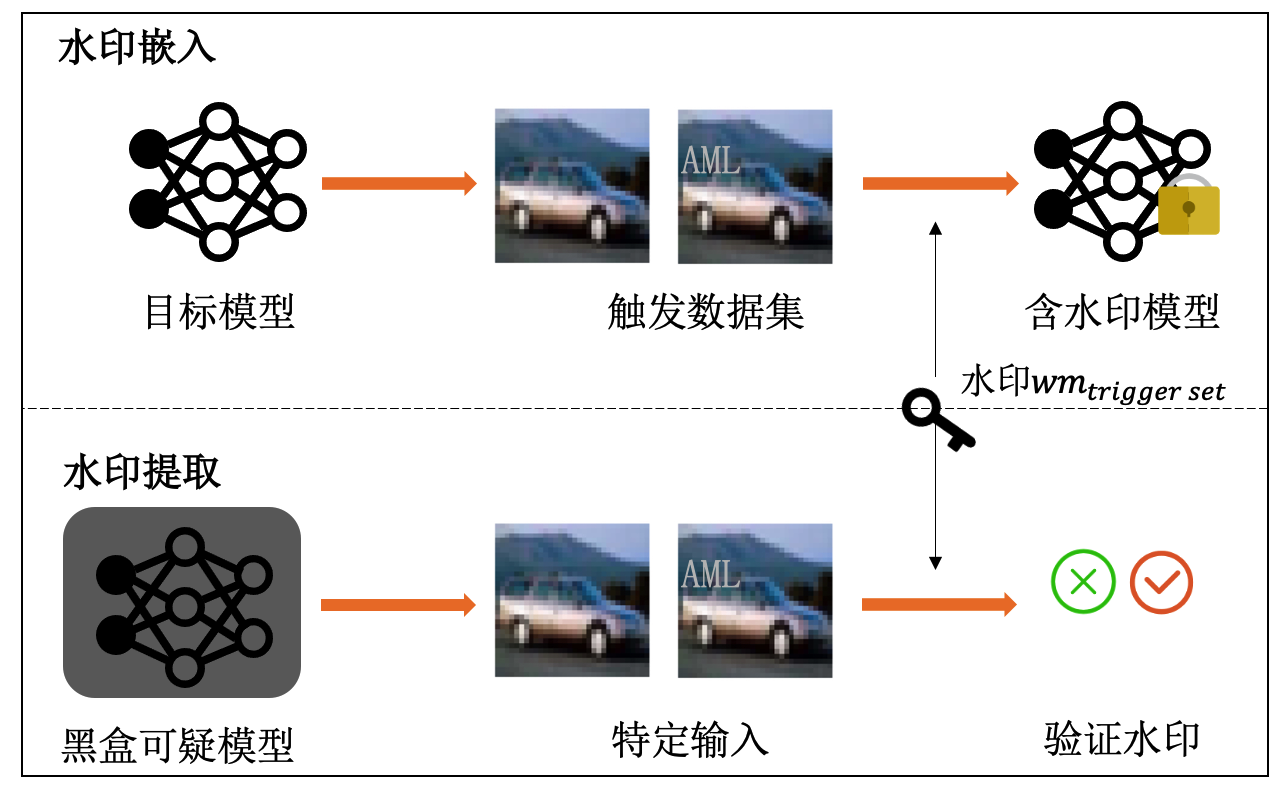
图10.2.2 黑盒水印方法¶

相较于白盒水印，黑盒水印的灵活度更高，适用场景更广泛，具有一定的应用优势。根据黑盒水印嵌入的阶段，又可以进一步将黑盒水印大致分为训练期间水印嵌入和推理期间水印嵌入。

训练期间水印嵌入。 在模型训练期间，可以通过篡改训练过程在模型中嵌入后门水印，引入特殊的输入输出关联关系，使模型学到这种关联特征。在水印提取过程中，模型所有者可以根据模型在后门水印数据上的预测标签来验证模型版权，即如果嫌疑模型在后门数据上输出后门类别则证明其为窃取模型。

Zhang等人 (Zhang et al., 2018) 在2018年首次提出利用后门嵌入的方式实验黑盒后门水印。模型持有者选取部分数据加入水印后门触发器（比如公司logo），生成触发数据集（trigger dataset）\(D_{\text{wm}}\)，并将触发数据对应的标签修改为后门标签（特定的错误标签），使得触发数据集具备”水印-后门类别”的对应信息。然后将后门数据集加入原始训练集，并在聚合后的数据集上训练模型。模型会在训练过程中学习到数据集\(D_{\text{train}}\cup D_{\text{wm}}\)中的水印触发器与后门类别之间的对应关系。

对基于后门的水印方法来说，最重要的是如何构建有效的触发数据集。为此，Zhang等人提供了三种水印（触发数据集）生成算法：（1）在原始图像上嵌入有意义的内容（\(\text{wm}_{\text{content}}\)）；（2）在原始图像上添加无意义噪声（\(\text{wm}_{\text{noise}}\)）；（3）直接使用无关图像（\(\text{wm}_{\text{unrelated}}\)）。这三种不同的构建方案可以让模型所有者根据不同的需求生成不同类型的水印。与此同时，Adi等人 (Adi et al., 2018) 也提出类似的模型水印方法，让模型故意输出特定的错误标签，从而来判定模型所有权。

Le等人 (Le Merrer et al., 2020) 在2020年提出了一种零比特水印方法。该方法利用决策边界附近的对抗样本构建触发数据集，并将这些对抗样本分为被分类器正确分类的有效对抗样本和被分类器错误分类的无效对抗样本。此方法通过微调来修改决策边界，使无效对抗样本变为有效对抗样本。因此，如若模型被窃取，模型所有者可使用触发数据集检验可疑模型的决策边界，进而确认模型版权。

在上述模型水印方法中，水印学习和原任务往往相互独立，所以攻击者可以在不影响模型原始性能的情况下轻易移除水印。为此，Jia等人 (Jia et al., 2021) 在2021年提出纠缠水印嵌入(entangled watermarking embeddings, EWE)方法，使得水印数据和原任务数据可以激活相同的神经元。该方法采用软最近邻损失函数（soft nearest neighbor loss, SNNL） (Frosst et al., 2019) 来衡量模型在水印数据和原任务数据上所学特征之间的纠缠，使得模型同时学习水印和原任务两种数据分布。SNNL损失函数的定义如下：

(10.2.10)¶\[\begin{aligned}\text{SNNL}(X,Y,T) = -\frac{1}{N} \sum_{i=1}^{N} \log \left( \frac{\sum\limits_{ \mathop{j \neq i}\limits_{y_i=y_j}} e^{-\lVert ( x_i- x_j) \rVert^{2}/T}}{\sum\limits_{ k \neq i} e^{-\lVert ( x_i- x_k) \rVert^{2}/T}} \right).\end{aligned}\]

基于SNNL训练的模型让窃取者无法在不影响模型性能的情况下擦除水印。因此，EWE方法有效的提高了模型水印技术在面对“模型窃取+水印擦除”攻击时的鲁棒性。

推理期间水印嵌入。 推理期间嵌入水印的思想比较巧妙，模型所有者在模型部署使用过程中，在返回给用户的输出中加入包含触发器的预测信息，让攻击者窃取出一个具有水印的模型。

2021年，Szyller等人 (Szyller et al., 2021) 提出神经网络动态对抗水印方法（dynamic adversarial watermarking of neural networks, DAWN）。DAWN算法不会干涉模型的训练过程，而是在推理阶段为来自API接口的查询动态嵌入水印。DAWN不仅可以识别可疑模型是否侵犯模型版权，还可以识别用户是否利用API返回的输出窃取模型。具体来说，攻击者\(A\)给定输入样本\(x\)，DAWN会根据用户查询次数动态返回正确预测\(f( x)\)或错误预测（触发数据集）\(f_b( x)\)，且\(f( x) \neq f_b( x)\)。因此，攻击者在窃取模型时会被误导，自己主动向替代模型\(f'( x)\)中植入后门关联关系\(( x,f_b( x))\)。

在水印提取阶段，模型所有者可以利用触发数据集\(D_b=(X_b, f_b(X_b))\)来验证模型版权，即\(f'( x) = f_b( x) \neq f( x)\)。此过程可形式化为：

(10.2.11)¶\[\begin{aligned}S(X_b, f_b, f) = \frac{1}{\left| X_b \right|} \sum\limits_{ x \in X_b} \mathbb{1}(f( x) \neq f_b( x)),\end{aligned}\]

其中，\(S(X_b, f_b, f)\)计算触发数据集中后门和可疑模型不同结果的比例，\(f'(X_b)\)为可疑模型返回的预测结果。与在训练期间嵌入水印的解决方案不同，在DAWN方法中向替代模型中嵌入水印的是攻击者自己，而不是模型所有者。

由于此前模型水印的研究大多侧重于图像分类模型，Zhang等人 (Zhang et al., 2020, Zhang et al., 2021) 为底层（low-level）计算机视觉模型提出了一个通用的模型水印框架。该方法在模型后处理过程中加入水印模块，向受害者模型的输出\(f( x)\)中嵌入一个不可见水印，使得攻击者只能获得水印版本的输出\(f'( x)\)。在水印嵌入过程中，如果攻击者利用带有水印的输出\(( x, f'( x))\)窃取模型，则水印将被攻击者自己嵌入到替代模型中。在水印提取过程中，模型所有者可以利用相应的水印提取模块，从可疑模型的输出中提取水印，从而验证模型版权。

10.2.3.2. 模型指纹¶

前文介绍的模型水印方法是一种侵入式的模型版权保护方案，因为它需要往模型中植入信息；而模型指纹是另外一类非侵入式的模型版权保护方法。与生物学上的指纹唯一性类似，深度神经网络模型同样具有独一无二的指纹（属性或特征）。模型所有者通过提取模型指纹，使其与其它模型区分开来，从而验证模型的版权。与侵入式的模型水印不同，模型指纹不会干预模型的训练过程也不会修改模型的参数，因此不会影响受保护模型的功能和性能，也不会引入新的风险。

模型指纹分为指纹生成（fingerprint generation）和指纹验证（fingerprint verification）两个阶段。在指纹生成阶段，模型所有者基于模型的独有特性提取得到指纹。在指纹验证阶段，模型所有者将指纹样本（可以区别两个模型特性的样本）通过调用可疑模型的API接口，计算受害者模型和可疑模型在一个样本子集上的输出匹配率，从而验证模型版权。

决策边界指纹。2021年，Cao等人 (Cao et al., 2021) 首次提出模型指纹方法IPGuard，通过受害者模型的决策边界指纹验证模型版权。以分类器为例，不同的分类器有不同的决策边界，故模型所有者可以选择决策边界附近的数据点作为指纹数据点（如图图10.2.3 所示），从而对可疑模型模型进行指纹验证。

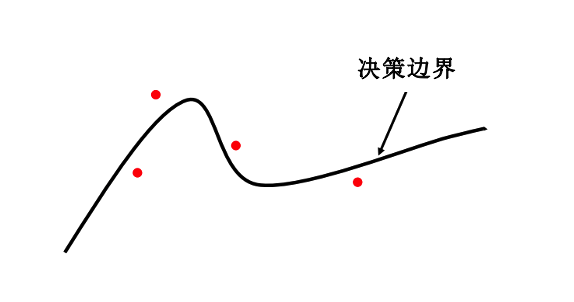
图10.2.3 IPGuard：使用边界上的数据点生成模型指纹 (Cao et al., 2021)¶

因此，对该方法来说，最重要的是寻找决策边界附近的指纹数据点，即分类器无法确定标签的数据点。

为了更快速的寻找到指纹数据点，IPGuard将查找分类器决策边界附近的指纹数据点转为下式中的优化问题：

(10.2.12)¶\[\begin{split}\begin{aligned}CB = \{ x|\exists i,j, i \neq j \, \text{and} \, g_i( x)=g_j( x) \geq \max\limits_{t \neq i,j} g_t( x)\}\\= \{ x|\exists i,j, i \neq j \, \text{and} \, Z_i( x)=Z_j( x) \geq \max\limits_{t \neq i,j} Z_t( x)\}\end{aligned}\end{split}\]

(10.2.13)¶\[\begin{aligned}\min\limits_{ x} ReLU(Z_i( x)-Z_j( x)+k) + ReLU(\max\limits_{t \neq i,j} Z_t( x)-Z_i( x)).\end{aligned}\]

在公式 (10.2.12) 中，\(CB\)为分类器决策边界，\(g_i( x)=\frac{\exp(Z_i( x))}{\sum^{C}_{j=1} \exp(Z_i( x))}\)为样本\(x\)被分类为标签\(i\)的概率，\(Z( x)\)为倒数第二层神经元的输出（即逻辑输出）。公式 (10.2.13) 的目的是寻找决策边界附近的指纹数据点，其中\(k\)为数据点到决策边界的距离。如果\(Z_i( x)=Z_j( x)\)，则意味着数据点\(x\)恰好在决策边界上。此外，当分类器由于数据分布随时间变化而定期更新时，模型指纹也需要定期更新。

另一种基于决策边界的模型指纹方式是由Lukas等人 (Lukas et al., 2019) 在2019年提出的可授予对抗样本（conferrable adversarial examples，CAE）方法。可授予对抗样本是指只在源模型和窃取模型之间迁移的对抗样本，相比之下，普通对抗样本往往可以迁移到任意模型。该方法将可授予对抗样本\(x\)作为模型指纹，使得替代模型\(f'\)与受害者模型\(f\)返回相同输出，即\(\mathop{\mathrm{arg\,max}}(f'( x)) =\mathop{\mathrm{arg\,max}}(f( x)))\)，同时使得参考模型\(f_R\)与受害者模型\(f\)返回不同输出\(\mathop{\mathrm{arg\,max}}(f_R(x)) =y\neq\mathop{\mathrm{arg\,max}}(f( x))\)，从而验证模型版权。其中，可授予对抗样本的定义如图图10.2.4 所示。

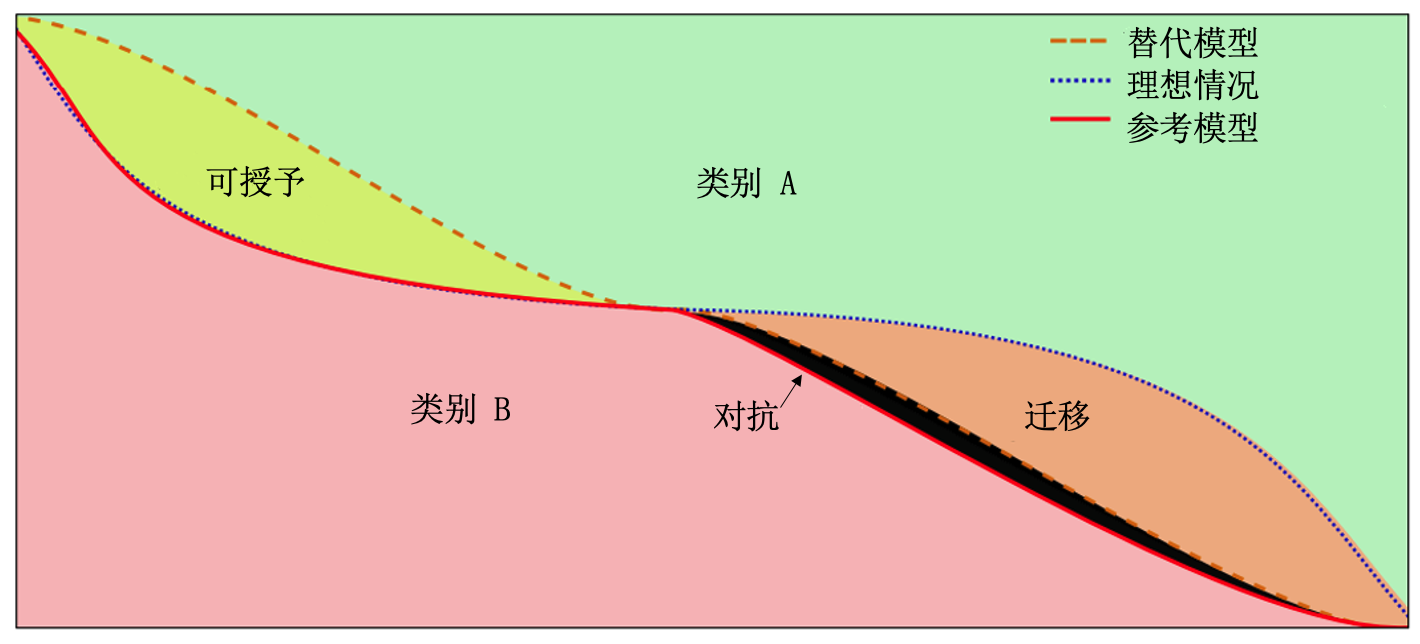
图10.2.4 可授予对抗样本 (Lukas et al., 2019) ：只向窃取模型迁移的对抗样本；可迁移对抗样本：可以向任何模型迁移的对抗样本¶

对CAE方法来说，最重要的是找到能最大化替代模型和参考模型之间差异的可授予对抗样本，此过程可形式化表示如下：

(10.2.14)¶\[\begin{split}\begin{aligned}\mathcal{L}( x, x_0) = \lambda_1 \mathcal{L}_{\text{CE}}(1, \max\limits_{t} [\sigma (Confer(f', f_R, x, t))])\\- \lambda_2 \mathcal{L}_{\text{CE}}(f( x), f( x_0)) + \lambda_3 \mathcal{L}_{\text{CE}}(f( x), f'( x))\end{aligned}\end{split}\]

(10.2.15)¶\[\begin{split}\begin{aligned}Confer(f', f_R, x, t) = Transfer(f', x, t) (1 - Transfer(f_R, x, t))\\Transfer(f', x, t) = \Pr\limits_{m \in \mathcal{M}}[m( x)=t].\end{aligned}\end{split}\]

在式 (10.2.15) 中，\(t\)为标签，\(Confer(f', f_R, x, t)\)为可授予分数，用于量化替代模型和参考模型之间的差异大小，\(Transfer(f', x, t)\)为可迁移分数由一组模型\(\mathcal{M}\)计算得来。在公式 (10.2.14) 中，三个损失项的目的是：(1）最大化对抗样本的可授予性，(2）最大化对抗性，(3）最小化受害者模型和替代模型之间的输出差异，从而生成可授予对抗样本\(x = x_0 + \delta\)作为模型指纹。与之前的模型指纹方法相比，可授予对抗样本模型指纹可以有效的减少误判。

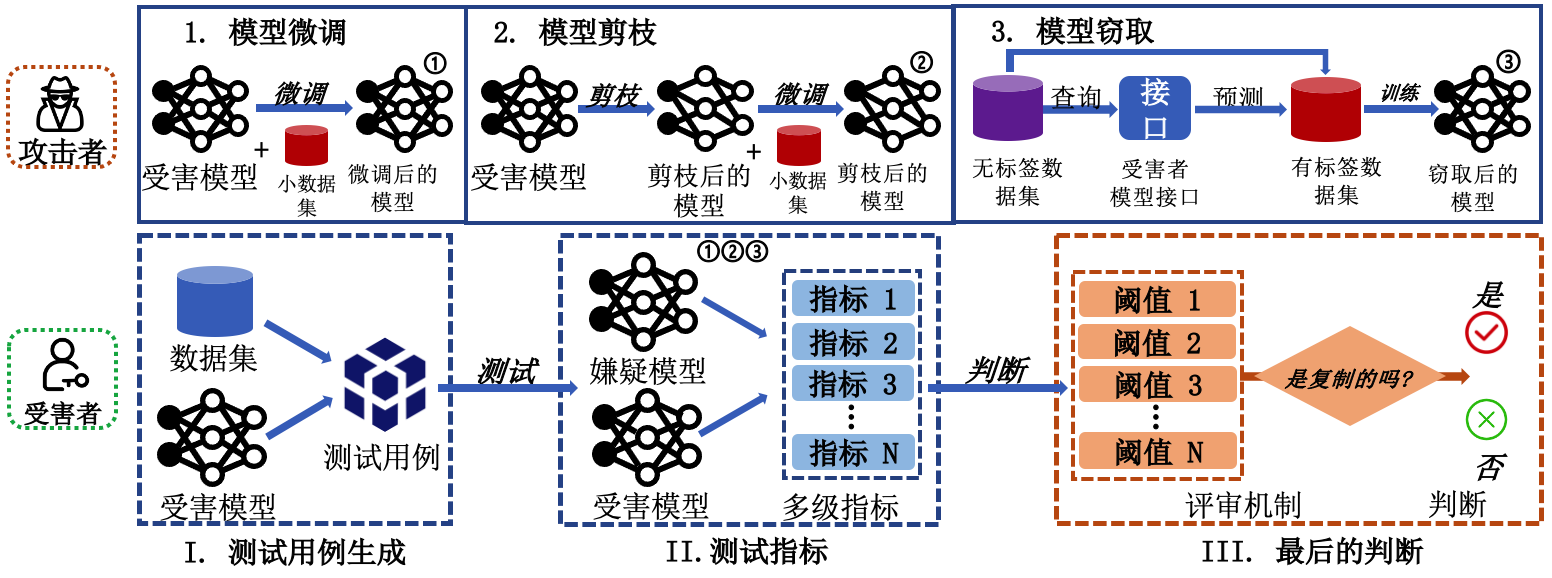
图10.2.5 DeepJudge框架 (Chen et al., 2022) ，上面一行为模型窃取行为示例，下面一行表示DeepJudge的三个步骤¶

基于测试的方法。Chen等人 (Chen et al., 2022) 提出将模型版权验证（也称模型溯源）问题当做验证一个模型是否是另一个模型的复制（copy）的问题，并提出一个基于模型测试（model testing）的版权保护和取证框架“深度法官”（DeepJudge）。如图图10.2.5 所示，DeepJudge由三部分组成：（1）采用现有的对抗攻击方法生成对抗样本，并构建一组测试用例；（2）测量可疑模型和受害者模型在测试用例上的行为相似度；（3）根据多个测试指标的结果投票判断模型所有权。

DeepJudge包含三类测试指标，即属性指标、神经元指标和神经层指标。如表图10.2.6 所示，根据不同的测试指标设置，DeepJudge同时支持白盒测试和黑盒测试。其中，白盒测试可以访问可疑模型的中间层结果和输出概率向量，而黑盒测试只能查询可疑模型以获得概率向量或预测标签。如果可疑模型是受害者模型的衍生，则可疑模型与受害者模型在某些测试指标上的会特别的接近，当大部分指标都认为两个模型接近时，可疑模型即为窃取模型。

图10.2.6 DeepJudge测试指标¶

DeepJudge可以被理解为是一种集成模型指纹（ensemble model fingerprint）方法，即综合多种指纹特征（即测试指标）和指纹数据（即测试用例）来构造一个更加系统全面的证据链。已有模型指纹方法可与DeepJudge提出的六种指标进行结合得到更全面的模型指纹保护方法。这一思想对模型水印也适用，可以通过构造多种不同类型的水印来达到更准确的模型溯源。

值得注意的事，目前的模型指纹方法，甚至包括模型水印的方法，都面临两个重要的缺陷：

鲁棒性较差；
衍生关系难判定。

在鲁棒性方面，一些常见的攻击，比如对抗攻击、适应性攻击等，可以很轻易的破坏水印和指纹的提取与验证过程。这意味着模型版权保护需要走“多管齐下”的路径，不管是水印还是指纹，需要多样化组合使用，让攻击者很难同时攻破所有的验证。判定衍生关系可能是人工智能模型知识产权保护所面临的最大的挑战。在很多情况下我们可以很容易的验证两个模型是否同源，但是无法鉴定二者的衍生关系，也就无法确定模型的原始归属。基于模型水印的方法在这方面尤其脆弱，因为攻击者完全可以在窃取模型后安插一个新的水印，然后宣称自己的水印才是先植入的，所以自己才是模型的真正拥有者。指纹类的方法虽然对此类的攻击具有一定的鲁棒性，但它们也无法确定两个模型之间的衍生关系。实际上，人工智能模型的学习过程本就是无序的，无法判断知识学习的先后顺序。不过，在实际的法律诉讼中，双方可以通过其他方面的证据（如模型训练记录）来侧面的解决这个涉及到“先后”的问题。

10.3. 本章小结¶

本章主要介绍了模型窃取攻击和防御方法。其中，章节 10.1节介绍了三类模型窃取攻击，包括基于方程式求解的窃取、基于替代模型的窃取和基于元模型的窃取。章节 10.2节介绍了三类有针对性的窃取防御方法，包括信息模糊、查询控制和模型溯源。比较前几个章节介绍的对抗攻防和后门攻防，不难发现模型窃取方面的研究还处于初级阶段，相关的研究工作并不多，还存在一定的方向性空白。实际上，现有模型窃取攻击还无法有效窃取大模型，所以难以给商用大模型带来威胁。所以要加快推进领域的发展就需要提出真正有威胁性的窃取攻击。当然，先进的模型知识产权保护系统永远是我们发展人工智能所要具备的关键技术，需要持续深入的探索。